Ford-Fulkerson Algorithm not "pushing back" flow

Question

I am told that with every flow network, the Ford-Fulkerson algorithm produces an execution that never decreases the value of the flow on any of the edges (i.e. never “pushes back” the flow on any of the edges). I am wondering how that can be possible. Can we choose augmenting paths that allow us to never "push back"?

Answer 1

No, it is not true that "the Ford-Fulkerson algorithm produces an execution that never decreases the value of the flow on any of the edges". If you look at the wiki article of Ford and Fulkerson method you will see the following pseudocode:

Algorithm Ford–Fulkerson
Inputs: Given a Network $G = (V,E)$ with flow capacity $c$, a source node $s$, and a sink node $t$
Output: Compute a flow $f$ from $s$ to $t$ of maximum value

$f(u,v) \leftarrow 0$ for all edges $(u,v)$
While there is a path $p$ from $s$ to $t$ in $G_f$, such that $c_f(u,v) > 0$
  for all edges $(u,v) \in p$:
    Find $c_f(p) = \min\{c_f(u,v) : (u,v) \in p\}$
    for each edge $(u,v) \in p$
      $f(u,v) \leftarrow f(u,v) + c_f(p)$ (Send flow along the path)
      $f(v,u) \leftarrow f(v,u) - c_f(p)$ (The flow might be "returned" later)

In the last line $f(v,u)$ is clearly decremented.

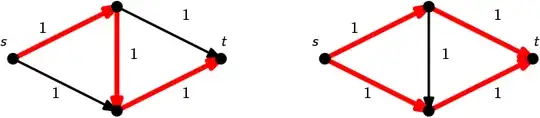
In the example below one will have to decrease flow in the middle edge to get max-flow. There is no other way.

If you want to know, if there exist a sequence of augmenting paths that never decrease the flows, then the answer is possibly yes. Proof might be non-trivial though.