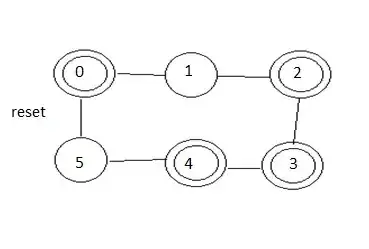
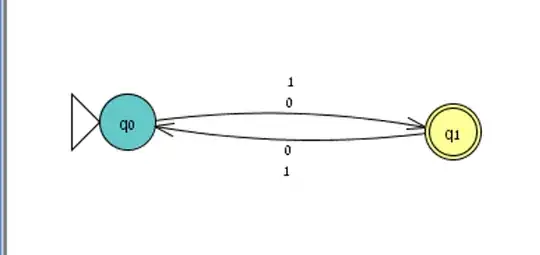
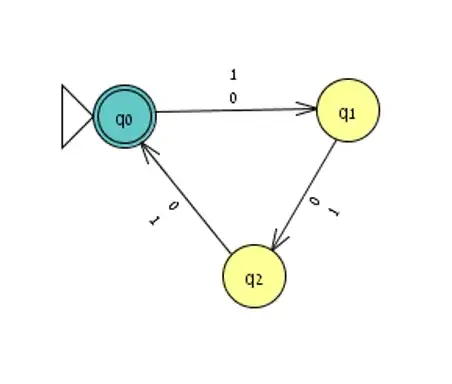
I am trying to create a DFA and a regex for this kind of exercise:
$A = \{w ∈ \{0, 1\}^* |\text{length of w is a multiple of 2 or 3}\}$. I tried to do one for $2$ and one for $3$ and then combine them, but it didn't seem to work cause I miss some cases for example $6,7$ or so. Any help would be gratefully received :D
Creating a state machine for each and combining the two is not a bad idea. To create a state machine accepting words having length N you can have each state represent the current length mod N.
After creating the two machines you can add a state having two epsilon transitions to the starting states of both machines. This gives a NFA accepting your language.
In a final stage you use the subset construction algorithm to convert the NFA you got into a DFA.
2 4 6 8 10 12 14 16 18...
.3 .6 .9 ... 12 .. 15 .18
Observe, that multiples of 2 and 3 meet after 6 numbers. So, you can think of resetting the 'counter' for every 6 symbols.
0 is the start state. For every 6 symbols, it resets to 0.
Constructing individually for 2 and 3, and then combining works well for "NFA". But, you need to convert that NFA back to DFA.
Regular Expression, in case of NFA will be (0|1+0|1)*|(0|1+0|1+0|1)*.
In case of DFA will be, ... not so early.
Constructing the regular expression from it a bit hectic. You need to follow the rules. (See here and here). The concept is called state removal method.
Hint:
buid the unity automata between those two, the first one accepts all the words with even length, and the second one accepts all the words above the alphabet such that $|w|\bigg|_{3}$
