I have been following the third edition of Introduction to Algorithms (by Cormen, Rivest, et al.), and have been studying the deletion algorithm for red-black trees. However, I am confounded at the moment while I am trying to delete a node from the tree.
The algorithm could be found at Page No. 324, third edition, Introduction to Algorithms,(CLRS).
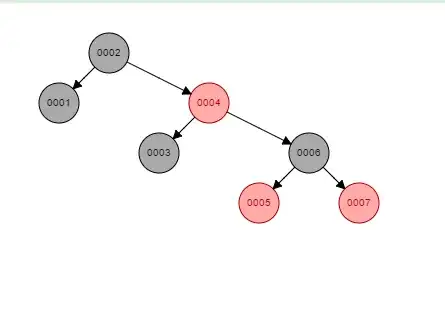
Suppose I have a red-black tree as follows:
This RB TRee was constructed by inserting the number 1 to 7 in non-decreasing order (i.e. 1,2,3,4,5,6,7).
Suppose we wish to delete the root of the tree, node 2.
Then as per the delete algorithm, on page-324,
1. y = z (i.e. y = ROOT of the tree)
2. y-original-color = BLACK
3. z.left exists, skip lines 4-5
6. z.right exists, skip lines 7-8
9. Now y = tree-minimum(z-right), i.e. y is a pointer to 3
10. y-original color = BLACK
11. x = y.right (i.e. T.NIL only)
12. y's parent = pointer to 4, which is not z (i.e. ROOT), skip line 13
14. Else transplant y with y.right, i.e. left of '4' is T.NIL now
15. Lines 15-16 fix the new parent issue for the transplanting node
17. Line 17 transplants z (i.e. the ROOT) with the pointer y, i.e. 3 is the root now
18. Lines 18-21 fix the parent and left child issue for the new ROOT
21. as y-original-color is BLACK, call the RB-DELETE-FIXUP function for x
As x is T.NIL, this is passed as an argument for the RB-DELETE-FIXUP function. However, there is an issue.
- How can we claim the parent of this x, i.e. the T.NIL, for the purpose of finding its sibling?
- Even if we claim that 4 be the parent of this x, and 6 be the sibling (as per the diagram), then the deletion falls under none of the categories mentioned in the book since 6 is a BLACK parent and both of its children are RED.
I have been following the algorithm and have been quite confounded by this case. Maybe there is a misinterpretation on my end regarding following the algorithm. Any help in this regard would be appreciated.