Does Thompson's algorithm produce optimal NFAs?

Question

I'm using Thompson's algorithm to convert from a regular expression to a NFA. Is Thompson's algorithm guaranteed to always output a minimal NFA, i.e., a NFA with the smallest possible number of states?

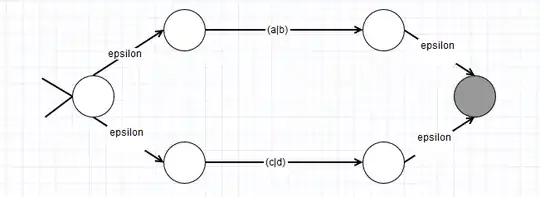
For instance, consider this example. I have the regular expression $(a|b)$. According to this website, Thompson's algorithm converts it to the following NFA:

   o--->o
  /ε  a  \ε
>o        O
  \ε  b  /ε 
   o--->o

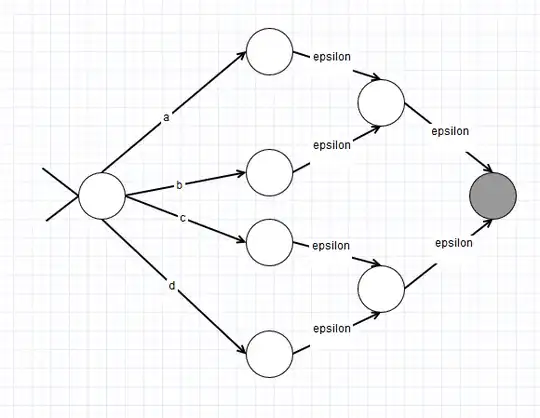
However, the following NFA is smaller and seems like it would also be equivalent:

   o
 a/ \ε
>o   O
 b\ /ε 
   o

Why doesn't Thompson's algorithm output the latter NFA? What did I miss here? Is that Thompson's construction algorithm not optimized at all?

Answer 1

Minimizing NFAs is known to be PSPACE-hard: Meyer and Stockmeyer showed that given an NFA, it is PSPACE-hard to find the size of the minimal equivalent NFA, and Jiang and Ravikumar showed that given a DFA, finding the size of the minimal equivalent NFA is PSPACE-hard. Later some hardness of approximation results were proved, showing that it is even hard to approximate the size of the minimal equivalent NFA. See these lecture notes by Artem Kaznatcheev for more details.

Since a regular expression can be converted to an NFA of comparable size using Thompson's algorithm, these hardness results show that we can't expect any efficient algorithm to convert an regular expression to a minimal-size NFA.

Answer 2

I had this same doubt when I was studying the Thompson's construction. As I see I am not the only one, I will try to solve the mystery.

Consider the regular expression: $$(a|b)|(c|d)$$

With Thompson's construction we generate first:

and then

Now let's use the noxwox's construction that you suggested. First we have:

And finally:

Can you see the difference? I had a first suspicion watching these two results. Then I reviewed the Thompson's constructions and I noticed something interesting. We can see the NFAs as directed graphs and the Thompson's construction guarantees a graph whose nodes have at most two successors.

So here starts my conclusion: Generating the data structure to store a NFA obtained by Thompson's construction is very easy because it is a set of nodes with two pointers each. If we use nowox's construction we don't know a priori the numbers of successors of each node and we have to change dynamically the amount of memory reserved for each node or be inefficient in the memory management. From this point of view the Thompson's construction algorithm guarantees a graph that is easy and fast to generate in a computer and I think that the additional computational cost of having more states than the NFA generated by nowox's construction is overshadowed by the backtracking mechanic of the NFAs.

Answer 3

Thompson's algorithm has no chance to output an optimal NFA, simply because a regular language can be given by several different regular expressions. Just try the regular expression $(a + b)^*(a + b)^*(a + b)^*$ on the tool given in reference. You will end up with a 22-state NFA, very far from the optimal 1-state NFA.

Answer 4

The minimal NFA for an regular expression (a|b) as you described would be below:

    a, b
>o ------> O

Basically this automaton can be produced by Antimirov's construction based on partial derivatives of regular expressions. For this construction you need a procedure to determine the equivalence of two regular expressions, which is known to be hard (Sorry no magic here!). However, if you relax the absolute minimality guarantee, you can use a procedure determining similarity of two regexs, which is efficient, so you can construct a near-minimal NFA.

A starting point for derivatives of regular expressions can be found here: http://www.mpi-sws.org/~turon/re-deriv.pdf