Prove correctness of DFA ending with ab

Question

I have the following deterministic finite automaton and I am need to prove correctness of the claim that this automata accepts $\{wab \mid w\in \{a,b\}^*\}$

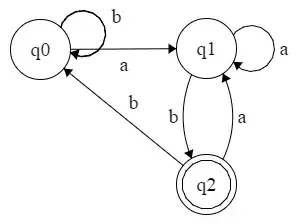
I know that I need to prove by induction on the length of the word but I am not sure how to do the induction step.

My try:

Anchor: After processing the only string of length zero, ε, the automaton is in state $q_0$ as claimed.

Hypothesis: After reading a string u the automaton is in state $q_1$ iff $u=xa$, and in state $q_2$ iff $u=xab$ and in $q_0$ iff $u=ε$ or $u=xb$. The claim holds for input fragments of length up to n.

Step: Any string $v$ of length $n+1$ is either $v=ua$ or $v=ub$

We split to cases:

1. $v=ua$ : According to the hypothesis- if $u$ ends with $b$ then it must be either in $q_0$ or $q_2$ - there for if we call $a$ after that we get to $q_1$ so $ua$ is not accepted. Also, if $u$ ends with $a$ then it must be in $q_1$ - there for if we call $a$ after that we get to $q_1$ so $ua$ is not accepted.
2. $v=ub$ : According to the hypothesis- if $u$ ends with $b$ then it must be either in $q_0$ or $q_2$ - there for if we call $b$ after that we get to $q_0$ so $ub$ is not accepted. Also, if $u$ ends with $a$ then it must be in $q_1$ - there for if we call $b$ after that we get to $q_2$ so $ua$ is accepted.

Answer 1

There is no induction needed. There is only one transition reaching the final state $q_2$, namely $q_1 \xrightarrow{b} q_2$. Furthermore, every transition reaching $q_1$ is labelled by $a$. It follows that every word accepted by the automaton has to end by $ab$. It remains to prove that, conversely, any word of the form $uab$ is accepted. After reading $u$ from the initial state $q_0$, you reach one of the three states $q_0$, $q_1$ or $q_2$. It suffices now to observe that $q_0 \xrightarrow{ab} q_2$, $q_1 \xrightarrow{ab} q_2$ and $q_2 \xrightarrow{ab} q_2$. Thus $q_0 \xrightarrow{uab} q_2$ in all cases, which means that $uab$ is accepted.

Answer 2

The induction hypothesis can look like: "after reading a string $u$ the automaton is in state $q_1$ iff $P_1(u)$, and in state $q_2$ iff $P_2(u)$." I leave it to you to determine what are the properties $P_1$ and $P_2$.