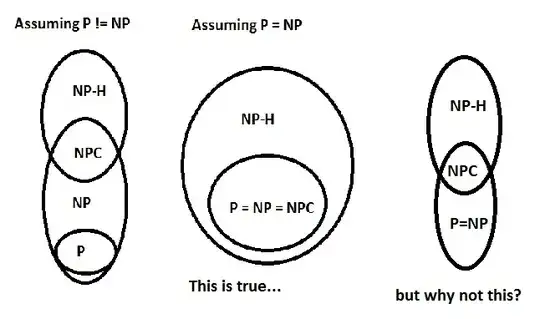
If P = NP, why does P = NP also then equal NP-Complete?
I.e. Why would it then be the case that P = NP = NP-Complete?
Assuming P != NP , there were problems in NP not in NP - Complete. When P = NP, all NP problems are actually now P.
Shouldn't there still be P = NP problems not in NP - Complete?