8

This is an exercise problem (Ex.3) from the excellent lecture note by Jeff Erickson Lecture 20: Minimum Spanning Trees [Fa’13] .

Prove that an edge-weighted graph $G$ has a unique minimum spanning tree if and only if the following conditions hold

  • For any partition of the vertices of $G$ into two subsets, the minimum-weight edge with one endpoint in each subset is unique.

  • The maximum-weight edge in any cycle of $G$ is unique.

Consider the "$\Rightarrow$" direction and the following graph $G$.

mst

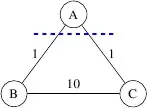
$G$ has a unique MST. However, for the partition $\{A\}$ and $\{B,C\}$, the minimum-weight crossing edge is not unique.

Did I misunderstand some points? Or if there are flaws in the theorem, how can we fix it?

hengxin
  • 9,671
  • 3
  • 37
  • 75

1 Answers1

0

Answer my own question by simply copying the comment made by @JeffE, the author of the lecture note：

Oops! Yes, this is a bug. (Note to self: Change every instance of "Prove" to "Prove or disprove".) – JeffE

hengxin
  • 9,671
  • 3
  • 37
  • 75