How to determine the set of numbers read by a DFA from one state to another?

Question

Using the Deterministic Finite Automaton (Q, Σ, Δ, q_0, F):

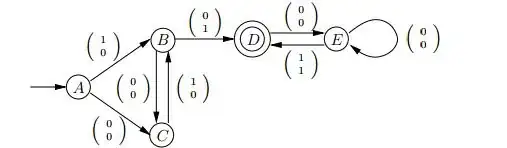
Alphabet: Σ is {(0 0), (0 1), (1 0), (1 1)}

Definition of Δ to strings recursively:

Δ*(q, ε) = q for all q ∈ Q

Δ*(q, xa) = Δ(Δ*(q, x), a) for all q ∈ Q, x ∈ Σ*, a ∈ Σ

Given a string, s ∈ Σ*, we define left(s) and right(s) to be the numbers represented in custom binary numbers by the reverse of the left and right rows of bits in s. For example, if

s = (1 0)(0 0)(0 1)(1 0)(0 0)(1 1)

then left(s) = n(s) = n(101001) = 19 and right(s) = n(s) = n(100100) = 16 where

$\sum_{i=1}^L s_i \bullet F_i $ where s is of length L.

and s = $s_L$$s_{L-1}$$s_{L-2}$...$s_1$ for s in n(s)

also the Fibonacci numbers start off as follows:

$F_0$ = 1

$F_1$ = 1

$F_n$ = $F_{n-1}$ + $F_{n-2}$ for n >= 2

Questions:

(a) If s is a string of length L and Δ*(A, s) = B, state a very simple arithmetic expression (in terms of L) for left(s).

(b) If s is a string of length L and Δ*(A, s) = C, state a very simple arithmetic expression (in terms of L) for left(s).

(c) Prove by induction on n: For all L >= 1, and every string s of length L, my answers to part (a) and (b) are correct.

This is a question for some homework and I have no idea where to start. For parts a and b I thought I'd use the formula for n(s) for something like this:

$\sum_{i=1}^L top(s_i) \bullet F_i $, but this formula doesn't take into account the transition from A to B or A to C. I'm not completely sure about what the expression should calculate either the string or the number?

Answer 1

For part (a) of your question, you want to know which input strings will take you from state $A$ to state $B$. We'll ignore the right element (the bottom of your pairs, in your picture), since it's always $0$ for the transitions we're interested in.

We can get from $A$ to $B$ directly, on input $1$, or we can go from $A$ to $B$ through $C$ on input $01$. In either case, once we're in state $B$, we can get back to there on input $01$. In other words, the input strings that take you from the start to state $B$ are $$ 1, 101, 10101, 1010101, \dotsc \qquad\text{or}\qquad 01, 0101, 011010, 01101010, \dotsc $$ Reversing these strings, we have $$ 1, 101, 10101, 1010101, \dotsc \qquad\text{or}\qquad 10, 1010, 101010, 10101010, \dotsc $$ For the odd-length strings, the values in this Fibonacci base representation will be $$ \begin{array}{lccccl} \text{value} & F_1 & F_1 + F_3 & F_1+F_3+F_5 & F_1+F_3+F_5+F_7 & \dotsc\\ \hline \text{length} & 1 & 3 & 5 & 7 & \end{array} $$ and we can get a similar result for the even-length input strings, only in this case we'll have values like $F_2+F_4+F_6$ for the length 6 input string. In simple terms, the value for length $k$ inputs, $v(k)$, will be $$ v(k) = \begin{cases} F_1 + F_3 + F_5 + \dotsm F_n & \text{ if $k$ is odd}\\ F_2 + F_4 + F_6 + \dotsm F_n & \text{ if $k$ is even} \end{cases} $$ Now you have a bit of work to do on your own. Compute the values $v(k)$ for, say, $k = 1, 2, 3, 4, 5$ and look at the results. If you stare at the values for a while, you might notice that they're almost equal to one of the Fibonacci numbers, except for the addition or subtraction of a constant. That'll be the answer you're looking for, and you'll find that it is indeed simple.

For part (b), do the same sort of thing, and, finally, for both of these parts, proving that your guesses were correct by induction on the lengths, $k$, shouldn't be too difficult.