What does it mean to prove that a set of binary integers is regular?

Question

I'm not exactly sure what this question is asking me to do:

Show that the set of binary integers (given as strings over $\{0, 1\}$) that are divisible by $3$ is regular, by giving a DFA that recognizes it. Leading 0s are allowed. The empty string should be accepted. Briefly explain your answer.

Is this asking me to construct a DFA where the set of binary integers add up to be divisible or the number of elements is divisible?

I understand that by constructing the DFA I prove that it is regular.

Answer 1

The question asks you to construct a DFA for the language

$$L = \{x \in \{0,1\}^* : x \text{ is the binary representation of an integer that is divisible by three}\}.$$

In other words, the DFA should accept a string if and only if this string is the binary representation of a number that is divisible by three.

Answer 2

The question want us to design a Deterministic Finite Automaton (DFA) that accepts Binary Representation of Integers that is divisible by 3.

$\mathcal{L}=\{x\in\{0,1\}^∗:x$ is the binary representation of an integer that is divisible by three$\}$

A word $w=a_{1}a_{2}...a_{n}\in \Sigma ^{*}$ is an accepting word for the automaton if $\overline {\delta }(q_{0},w)\in F$, that is, if after consuming the whole string $w$, the machine is in an accept state.

Approach : We need to divide the Binary Representation of Integer by 3, and note the remainder. If after consuming/scanning [From Left to Right] the entire string, remainder is Zero, then we should end up in one of the Final States, else we should be in Non-Final States.

Now, DFA is defined by Quintuple$/5$-Tuple $(Q,F,q_0,\Sigma,\delta)$. We will obtain these five components step-by-step.

---

$Q$ : Finite Set of States
We need to note remainder. On dividing any integer by $3$, we can get remainder as $0,1$ or $2$. Hence, we will have Three States $Z, V$ and $T$ respectively. $$Q=\{Z,V,T\}$$ If after scanning certain part of Binary String, we are in state $T$, this means that integer defined from Left to this part will give remainder $T$wo when divided by $3$. Similarly, $V$ for remainder $1$, and $Z$ for remainder $0$.
$\hspace{6cm}$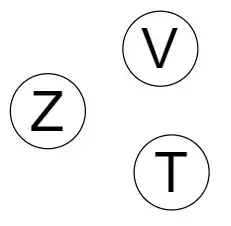

Now, we can write these three states (by Euclidean Division Algorithm) as

$Z=3m\qquad V=3m+1\qquad T=3m+2\qquad$ where $m \in \mathbb{Z}$

---

$F :$ a set of accept states, $F\subseteq Q$
Now we want strings which are divisible by $3$, or which gives remainder $0$ when divided by $3$, or which after complete scanning should end up in state $Z$, and gets accepted. Hence, $$F=\{Z\}$$
$\hspace{8cm}$

---

$q_0$ : an initial/start state $q_0\in Q$
An Empty String $(\varepsilon)$ directly gets into $q_0$. And $\varepsilon$ should get accepted. Thus $q_0$ be one of the Final State. And since we have only one Final State. Hence,

$$q_0=Z$$ $\hspace{6cm}$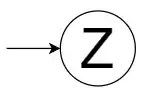

---

$\Sigma :$ Alphabet (a finite set of input symbols)
Since we are scanning/reading a Binary String. Hence,

$$\Sigma=\{0,1\}$$

---

$\delta :$ Transition Function $(δ : Q × Σ → Q)$
Now this $\delta$ tells us that if we are in state $a\in Q$ and next input to be scanned is $b\in \Sigma$, then at which state $c\in Q$ should we go.

In context of this problem, if the string upto this point gives remainder $1/V$ when divided by $3$, and if we append $1$ to string, then what remainder will resultant string give.

Now, this can be mathematically analyzed by observing how magnitude of a binary string changes on appending 0 and 1.

In Decimal (Base-$10$), if we add/append $0$, then magnitude gets multiplied by

$10$
Example : $64$, on appending $0$ it becomes $640$

Also, if we append $6$ to decimal, then

Magnitude gets multiplied by $10$, and then we add $6$ to multiplied magnitude.

In Binary (Base-$2$), if we add/append $0$, then magnitude gets multiplied by

$2$ (The Positional Weight of each Bit get multiplied by $2$)
Example : $(1010)_2$ [which is $(10)_{10}$], on appending $0$ it becomes $(10100)_2$ [which is $(20)_{10}$]

Similarly, In Binary, if we append $1$, then

Magnitude gets multiplied by $2$, and then we add $1$.
Example : $(10)_2$ [which is $(2)_{10}$], on appending $1$ it becomes $(101)_2$ [which is $(5)_{10}$]

Thus, we can say that for Binary String $x$,

• $x0=2|x|$
• $x1=2|x|+1$

We will use these relation to analyze three States

• Any string in $Z$ can be written as $3m$

  • On $0$, it becomes $2(3m)$, which is $3(2m)$, nothing but state $Z$.
  • On $1$, it becomes $2(3m)+1$, which is $3(2m)+1$, that is $V$.
    [This can be read as if a Binary String is presently divisible by $3$, and we append $1$, then resultant string will give remainder as $1$]
    $\hspace{3cm}$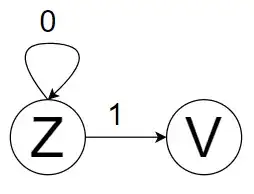

• Any string in $V$ can be written as $3m+1$

  • On $0$, it becomes $2(3m+1)=6m+2$, which is $3(2m)+2$, state $T$.
  • On $1$, it becomes $2(3m+1)+1=6m+3$, which is $3(2m+1)$, state $Z$.
    [If $m\in \mathbb{Z}$, then $(2m+1)\in \mathbb{Z}$]
    $\hspace{3cm}$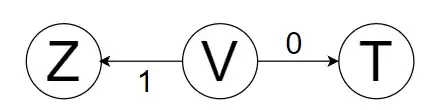

• Any string in $T$ can be written as $3m+2$

  • On $0$, it becomes $2(3m+2)=6m+4$, which is $3(2m+1)+1$, state $V$.
  • On $1$, it becomes $2(3m+2)+1=6m+5$, which is $3(2m+1)+2$, state $T$.
    $\hspace{3cm}$

---

Hence, the final DFA combining all Five Components is

Since, we have constructed DFA. Hence, the language $\mathcal{L}$ is regular.

---

Answer 3

Hint: Make three states, $q_0, q_1, q_2$, representing the fact that in state $q_i$ you have seen a string of 0s and 1s that, when interpreted as a binary number, represents a number with remainder of $k$ when divided by 3. For example, having read $\mathtt{00101}$, the FA would be in state $q_2$, since the binary string $\mathtt{00101}$ corresponds to the decimal value 5, which has a remainder of 2 when divided by 3.

Now fill in the transitions: If, say we're in state $q_2$ having read a string that corresponds to a number $n$, what state would the FA be on reading a $\mathtt{0}$? What happens when you add a zero to the right of the representation of $n$, going, say from $\mathtt{00101}$ to $\mathtt{001010}$? Use this idea to fill in all the transitions and then decide what the final state(s) should be.