Converting NFA to regular expression

Question

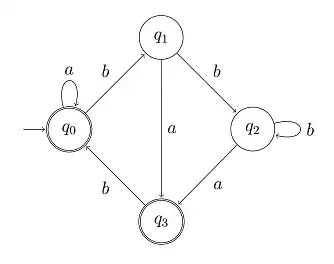
Here is the regular expression I made for it

This is my first answer, used the naive method aka don't know what am doin' method. $$ \epsilon \cup a^* \cup (a^*b) \left((a| b^*a) | \left( (a|(b^*a))ba^*\right) \right) ^* $$

this is my re-worked answer, with the state removal method.

$$ \left( a^* \cup (b)(a \cup bb^*a) \right) ^* $$

steps taken :

1. Add a new start state and a new final state.
2. Add epsi transitions to the new states.
3. Remove Q2
4. Link between Q1 and Q3 is now $a \cup bb*a$
5. Remove Q1
6. Add a new link between Q0 and Q3 with $ (b)(a U bb*a)$ label
7. Remove Q0 There are three paths. a*, the big regex and the start with epsi $\epsilon \cup a* \cup (b)(a \cup bb*a)$
8. Remove Q3
9. We get $\epsilon \cup \left( a^* \cup (b)(a \cup bb^*a) \right) ^*$ =$ \left( a^* \cup (b)(a \cup bb^*a) \right) ^*$

My questions are:

• Is my regular expression correct ?
• What happens if it loops ?

To be clear, let's say we have the string aababaaaaabab

I think that string is recognized by the NFA, but I'm not sure it is by my regular expression.

does the $^*$ at the end cover it correctly ?

ps: As suggested I moved this from math.se

Answer 1

For your specific problem, I propose a regular expression in a ad-hoc meth, and the outcome was: (notation comes from Regular Expressions)

(a*(b(b+)?ab?)?)*

I found it with the next methodology: moving from simple to more complex ( states to final states)

• To arrive to $q_3$, you need to put a
• This a comes from $q_1$ or $q_2$
• If it comes from $q_1$, use a b else it comes from $q_2$, so use one o more b's: b+
• But, $q_2$ comes from b too, so union these two possibilities, a comes from b((b+)?)
• For that, we have b(b+)?a in regular expression to go from $q_1$ to $q_3$
• Now, If you want to move from $q_3$ to $q_0$, you need a extra b, so use b?. This is the part of regular expression: b(b+)?ab?
• To start you probably have empty string, or a's or b to go from $q_0$ to $q_1$
• Above can achieve with a* and visit $q1$ or not visit is express like: a*(b(b+)?ab?)?
• Finally, you could have a nothing of that, or more than once this strings, so you should use *, and take as regular expression: (a*(b(b+)?ab?)?)*

Test Cases

I tested with the next strings and all match with the regex:

1. aaaaba
2. aababaaaaaa
3. abbbbbba
4. abbbbbbab
5. abbbbbbabaaaa
6. abbbbbbaba
7. bab
8. ba
9. babaaaa
10. aaaaa
11. bbba

In the other hand, you may be interested in consider algorithms to converting DFA to Regular expression, so you can find a dynamic programing algorithm, and the full description of this approach is given in the book of Models of Computation, Chapter 4. And other method, Brzozowski algebraic method. All above, because with the powerset constructive you can obtain a DFA from NFA.