1

I just came across an exercise which is to find a regular expression for the following automaton, such that the regular expression and the automaton generate the same language.

NFA

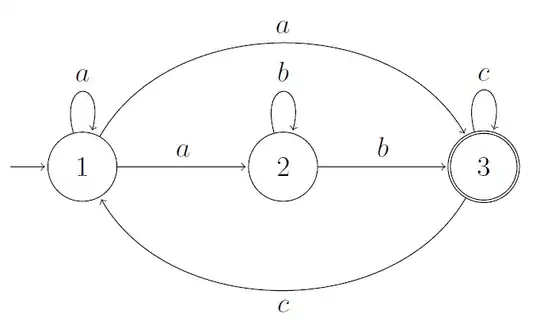
One solution presents the following expression:

$\qquad \displaystyle r_A = a^+b^+(c\mid ca^*b^+)^*$

However, can this be true? I think not, because the all words created from the regular expression will have at least one $b$ in it, whereas the automaton accepts words without $b$, such as $aaa$.

What is your opinion?

reinierpost
  • 6,294
  • 1
  • 24
  • 40
Erik
  • 181
  • 3

2 Answers2

2

In general, you can decide equivalence of regular expression and finite automaton using standard algorithms:

  • Construct an NFA from the regular expression,
  • Determinise and minimise both automata,
  • Check for equality (up to isomorphism).

These algorithms and proof that the minimal DFA of any regular language is unique (up to isomorphism) can be found in introductory textbooks.

If the underlying task is to "read off" a regular expression from an automaton, don't guess & proof but rather build the expression algorithmically to save time.

Community
  • 1
Raphael
  • 73,212
  • 30
  • 182
  • 400
0

You can use formal methods like the elimination method.

However, in this specific case, since there is only one accepting state, and all the paths are directed to it - We can look at each path from the initial state to the accepting state and characterize it using regular expression. Then, we can perform union over the expressions we got, and maybe more manipulations.

  • Path 1 - upper - $a^*ac^*$
  • Path 2 - middle - $a^*ab^*bc^*$
  • Path 3 - lower - $a^*cc^*$

We can unify the shared parts and get:

$a^*(a + ab^*b + c)c^*$

(Btw - It's not necessarily a minimal regular expression for the language).

Yuvi
  • 322
  • 1
  • 14