Why do low fitness individuals have a chance to survive to the next generation?

Question

I am currently reading and watching about genetic algorithm and I find it very interesting (I haven't had the chance to study it while I was at the university).

I understand that mutations are based on probability (randomness is the root of evolution) but I don't get why survival is.

From what I understand, an individual $I$ having a fitness $F(i)$ such as for another individual $J$ having a fitness $F(j)$ we have $F(i) > F(j)$, then $I$ has a better probability than $J$ to survive to the next generation.

Probability implies that $J$ may survive and $I$ may not (with "bad luck"). I don't understand why this is good at all? If $I$ would always survive the selection, what would go wrong in the algorithm? My guess is that the algorithm would be similar to a greedy algorithm but I am not sure.

Answer 1

The main idea is that by allowing suboptimal individuals to survive, you can switch from one "peak" in the evolutionary landscape to another through a sequence of small incremental mutations. On the other hand, if you only are allowed to go uphill it requires a gigantic and massively unlikely mutation to switch peaks.

Here is a diagram showing the difference:

Practically, this globalization property is the main sellling point of evolutionary algorithms - if you just want to find a local maxima there exist more efficient specialized techniques. (eg., L-BFGS with finite difference gradient and line search)

In the real world of biological evolution, allowing suboptimal individuals to survive creates robustness when the evolutionary landscape changes. If everyone is concentrated at a peak, then if that peak becomes a valley the whole population dies (eg., dinosaurs were the most fit species until there was an asteroid strike and the evolutionary landscape changed). On the other hand, if there is some diversity in the population then when the landscape changes some will survive.

Answer 2

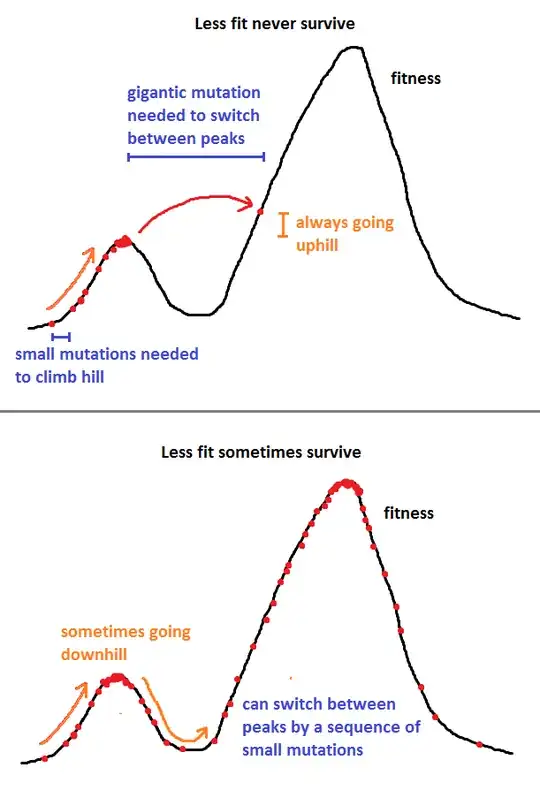
Nick Alger's answer is very good, but I'm going to make it a little more mathematical with one example method, the Metropolis-Hastings method.

The scenario that I'm going to explore is that you have a population of one. You propose a mutation from state $i$ to state $j$ with probability $Q(i,j)$, and we also impose the condition that $Q(i,j) = Q(j,i)$. We will also assume that $F(i)>0$ for all $i$; if you have zero fitness in your model, you can fix this by adding a small epsilon everywhere.

We will accept a transition from $i$ to $j$ with probability:

$$\min\left(1, \frac{F(j)}{F(i)}\right)$$

In other words, if $j$ is more fit, we always take it, but if $j$ is less fit, we take it with probability $\frac{F(j)}{F(i)}$, otherwise we try again until we accept a mutation.

Now we'd like to explore $P(i,j)$, the actual probability that we transition from $i$ to $j$.

Clearly it's:

$$P(i,j) = Q(i,j) \min\left(1, \frac{F(j)}{F(i)}\right)$$

Let's suppose that $F(j) \ge F(i)$. Then $\min\left(1, \frac{F(j)}{F(i)}\right)$ = 1, and so:

$$F(i) P(i,j)$$ $$= F(i) Q(i,j) \min\left(1, \frac{F(j)}{F(i)}\right)$$ $$= F(i) Q(i,j)$$ $$= Q(j,i) min\left(1, \frac{F(i)}{F(j)}\right) F(j)$$ $$= F(j) P(j,i)$$

Running the argument backwards, and also examining the trivial case where $i=j$, you can see that for all $i$ and $j$:

$$F(i) P(i,j) = F(j) P(j,i)$$

This is remarkable for a few reasons.

The transition probability is independent of $Q$. Of course, it may take us a while to end up in the attractor, and it may take us a while to accept a mutation. Once we do, the transition probability is entirely dependent on $F$, and not on $Q$.

Summing over all $i$ gives:

$$\sum_i F(i) P(i,j) = \sum_i F(j) P(j,i)$$

Clearly $P(j,i)$ must sum to $1$ if you sum over all $i$ (that is, the transition probabilities out of one state must sum to $1$), so you get:

$$F(j) = \sum_i F(i) P(i,j)$$

That is, $F$ is the (unnormalised) probability density function for which states the method chooses. You are not only guaranteed to explore the whole landscape, you do so in proportion to how "fit" each state is.

Of course, this is only one example out of many; as I noted below, it happens to be a method which is very easy to explain. You typically use a GA not to explore a pdf, but to find an extremum, and you can relax some of the conditions in that case and still guarantee eventual convergence with high probability.

Answer 3

The advantage of using a GA is that you are able to explore broader search spaces by following paths which come from potentially worse candidates. There should be worse candidates making it through in order to explore these different areas of the search, not many but definitely a few. If you start taking only the very best every time you remove this exploration aspect of the algorithm and it becomes more of a hill climber. Also only selecting the best constantly may lead to premature convergence.

Answer 4

Actually, selection algorithms take both approaches. One way is what you suggested and the other is that individuals with higher fitness are selected and those with lower ones are not.

The approach you pick for selection is also tailored to the problem you are trying to model. In an experiment back in school, we were trying to evolve card players by having them play games against each other (i.e. tournament selection). In such a scenario, we could very well just always favor $I$ over $J$ (from your example) because the 'luck' aspect is already in the game itself. Even if $F(i) > F(j)$ for any two $I$ and $J$, in any given round, purely by the way hands were dealt and how others played, $J$ could have won the round and thus we could end up with $F(j) > F(i)$. Keep in mind that a population is often large enough that one can afford to lose some good individuals and on the whole, it will not matter as much.

Since GAs are modeled around real-world evolution, when probabilistic distributions are used, they are primarily modeled around how real communities evolve in which sometimes individuals with lower fitness may survive whereas individuals with higher fitness may not (a crude analogy: car accidents, natural disasters etc. :-)).

Answer 5

its very simple, from one pov: sometimes higher-fitness "child" solutions can be born of lower-fitness "parent" solutions via either crossover or mutation (that actually is a lot of the theory of genetic algorithms). so in general one wants to seek/carry the higher-fitness solutions but too much emphasis on keeping/breeding only high-fitness solutions can lead to getting stuck in local minima and not searching the large "evolutionary landscape". actually one can make the "higher fitness cutoff" for survival as strict or lax as one wishes & experiment with how it affects quality of the final solution. both too-strict or too-lax cutoff strategies will lead to inferior final solutions. of course all this has some relationship to real biological evolution. there its more "environmental pressure/resource scarcity" that affects survival, and there it can be cyclical.