Building Simple Parse Trees

Question

I am trying to learn how to build parse trees.

I have watched videos and tried to do some on my own, but am a little lost.

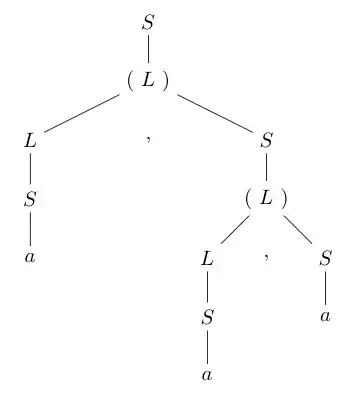
In this example, I am given the following:

$$ \begin{align*} &S\to(L) \\ &S\to a \\ &L\to L,S \\ &L\to S \end{align*} $$

and then I am told to draw a parse tree for the expression $(a,(a,a))$.

I know that the first $S$ is the start symbol, I know that since I am trying to draw it for a specific string, I should use the bottom up approach, but I am very confused.

Can the lines above also be written as $$ \begin{align*} &S\to(L)|a \\ &L\to L,S|S \end{align*} $$ or can they not be combined that way?

How would you write this tree? What confuses me the most is how to write the tree using the $L$ and $L,S$ but resulting in $(a,(a,a))$.

I would appreciate any explanation or demonstration offered.

Answer 1

The notation $S\to(L)|a$ is shorthand to $S\to(L)$ and $S\to a$, so you can rewrite the grammar in your equivalent form; I don't see how this makes things any different, since the two grammars are exactly the same.

The first step in writing a parse tree is coming up with a derivation. In the derivation below, I use boldface to indicate the non-terminal being expanded. $$ \begin{align*} \mathbf{S}&\to(\mathbf{L}) \\ &\to(\mathbf{L},S) \\ &\to (\mathbf{S},S) \\ &\to (a,\mathbf{S}) \\ &\to (a,(\mathbf{L})) \\ &\to (a,(\mathbf{L},S)) \\ &\to (a,(\mathbf{S},S)) \\ &\to (a,(a,\mathbf{S})) \\ &\to (a,(a,a)) \end{align*} $$ There are several different derivations which "feel" the same. For example, in this derivation I always expanded the left-most non-terminal, but you could just as well expand any other non-terminal. When you draw the derivation tree, all these derivations give rise to the same tree.

Here is the actual derivation tree, drawn by Rick Decker: