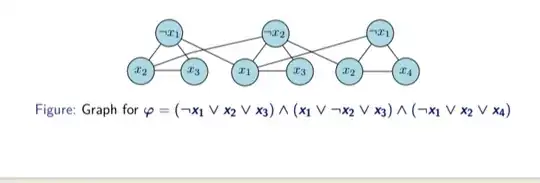
Main question is: I want to do reduction: $$\text{MAX-3SAT}\leq_p\text{MAX-INDSET}.$$
My tried so far:
But I know the reduction $\text{3SAT}\leq_p\text{Independent Set}.$
Input: Given a 3CNF formula $\varphi$.
Goal: Construct a graph $G_\varphi$ and number $k$ such that $G_\varphi$ has an independent set of size $k$ if and only if $\varphi$ is satisfiable.
$G_\varphi$ should be constructable in time polynomial in size of $\varphi$.
Interpreting $\text{3SAT}$:
There are two ways to think about $\text{3SAT}$:
- Find a way to assign 0/1 (false/true) to the variables such that the formula evaluates to true, that is each clause evaluates to true.
- Pick a literal from each clause and find a truth assignment to make all of them true. We will fail if two of the literals you pick are in conflict, i.e., we pick $x_i$ and $\neg x_i$.
We will take the second view of 3SAT to construct the reduction.
The Reduction:
$G_\varphi$ will have one vertex for each literal in a clause
Connect the 3 literals in a clause to form a triangle; the independent set will pick at most one vertex from each clause, which will correspond to the literal to be set to true
Connect 2 vertices if they label complementary literals; this ensures that the literals corresponding to the independent set do not have a conflict
Take $k$ to be the number of clauses
Correctness:
$\varphi$ is satisfiable iff $G_\varphi$ has an independent set of size $k$ (= number of clauses in $\varphi$).
$(\Longrightarrow)$Let $a$ be the truth assignment satisfying $\varphi$.
I Pick one of the vertices, corresponding to true literals under $a$, from each triangle. This is an independent set of the appropriate size.
$(\Longleftarrow)$Let $S$ be an independent set of size $k$
$S$ must contain exactly one vertex from each clause
$S$ cannot contain vertices labeled by conflicting literals
Thus, it is possible to obtain a truth assignment that makes in the literals in $S$ true; such an assignment satisfies one literal in every clause.
But I unable to do maximum variation, how to do reduction in maximum variation i.e. form MAX-3SAT to Maximum-Independent Set?