Optimizing node removal in a graph to achieve minimal edge weights while maintaining a certain total node weight

Question

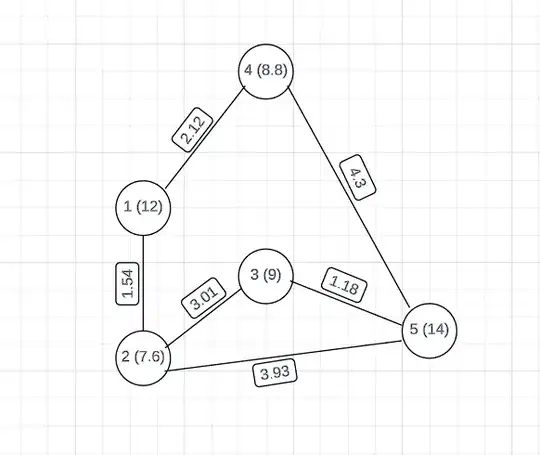
In the graph above with weighted edges and nodes (node weights in parenthesis), I have a goal of reducing total edge weight. I can achieve this by simply taking out nodes and thereby removing edges, however, I have a certain minimum total node weight I want to maintain in the graph network.

A simple (greedy) way of reaching that minimum total node weight while reducing edge weight as much as possible is to calculate the ratio of "adjacent edge weight/node weight" for each node and take out the node with the highest ratio, recalculate the ratio and again take out the node with the highest ratio, do this till the minimum total node weight is reached.

In a larger graph, there may exist different combinations of node removals that can achieve the same minimum total node weight. These different combinations would also probably leave different total edge weights after the minimum total node weight is reached. I'm thinking of a way to optimally search for the best combination of node removal that reaches this minimum total node weight with the lowest total edge weight left after the node removals.

A brute force approach may involve me running for loops to find all the possible node removal combinations and then selecting the one that achieves the lowest total edge weight. Is there an algorithm that can optimize this or how would you solve this?

I have zero background in CS, I'm a researcher in a different field that stumbled on this and can see some relevance in my work. Apologies if my explanation is not clear enough. I would appreciate any help with this.

Answer 1

The problem is NP-complete by reduction from the knapsack problem, so you should not expect any efficient algorithm that works correctly in all possible cases.

A plausible approach to solve this in practice is to formulate it as an instance of integer linear programming (ILP). In particular, define zero-or-one variables $x_v$, $y_{u,v}$ with the intended meaning:

• $x_v=1$ means vertex $v$ is retained; $x_v=0$ means vertex $v$ is deleted
• $y_{u,v}=1$ means edge $u,v$ is retained (i.e., $x_u=1$ and $x_v=1$); $y_{u,v}=0$ means edge $u,v$ is deleted (i.e., either $u$ is deleted or $v$ is deleted or both)

You can enforce constraints on the $x$'s and $y$'s to ensure that you get a valid solution to your problem:

• consistency: enforce $y_{u,v} = x_u \land x_v$ using the techniques in Express boolean logic operations in zero-one integer linear programming (ILP), i.e., $y_{u,v} \ge x_u + x_v - 1$, $y_{u,v} \le x_u$, $y_{u,v} \le x_v$.

• minimum node weight: enforce $\sum_v w_v x_v \ge m$, where $w_v$ is the weight of vertex $v$ and $m$ is the desired minimum node weight.

Then, your goal is to minimize the total edge weight $\sum_{u,v} w_{u,v} y_{u,v}$, where the sum ranges over all edges $(u,v)$ in the graph and $w_{u,v}$ is the weight of edge $(u,v)$. This is an instance of ILP, and hence you can try solving it with an off-the-shelf ILP solver, e.g., CPLEX or Gurobi. No guarantees whether this works well enough your particular problem instances, but give it a try, it might just do the trick.