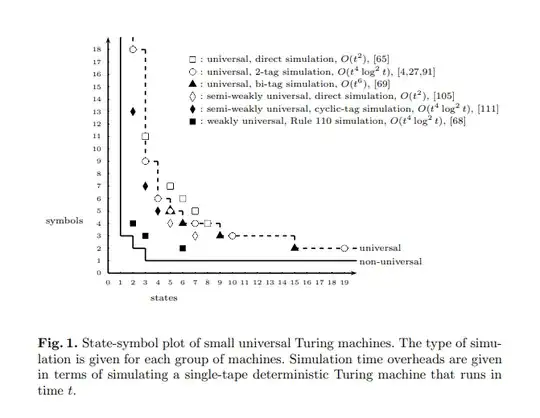
The paper The complexity of small universal Turing machines: a survey (.pdf) includes the following chart of the then (2011) smallest known Universal Turing Machines.
The ones marked as rectangles only require $O(t^2)$ steps to simulate another single tape turing machine (by the direct method) which is much more practical in terms of simulation (and possible construction) compared to the other polynomial ones.
Is $O(t^2)$ still the best known lower bound for these small machines or are improvements still possible or already known? Or has this result maybe been proven to be the optimum?
This answer seems to mention that
We know that we can implement $\mathcal{U}$ in such a way that if the computation $M(x)$ requires time $T$, then $\mathcal{U}(\langle M\rangle,x)$ requires time $O\left(T\log T\right)$.
and that
It seems that for single tape machines, it is not known whether this $\log T$ factor is necessary, [...]
Have these results been achieved in the context of small Universal Turing Machines as well?