Context:
While exploring the fundamentals of polyhedral optimization and attempting to explore a connection from the input Static Control Part (SCoP) to the iteration domain from birds eye view, I am confused about whether I am making the correct connections or not.
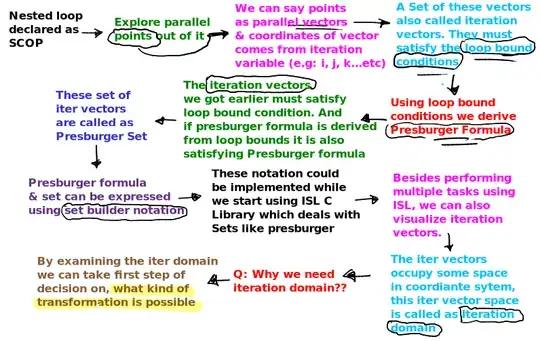
Explored connection map:
Example case:
Let's see a code snippet;
# SCOP
for i in range(1, 9): # 1 and 9 are loop bounds
for j in range(i+1, 10): # i+1 and 9 are loop bounds
# statement S
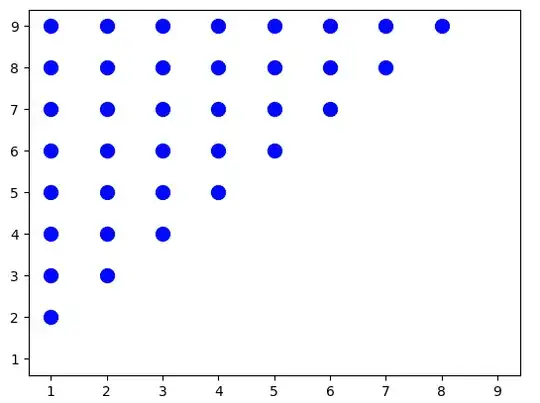
Triangle = isl.BasicSet("{S[i,j] : 0 < i < j <= 9}")
plot_set_points(Triangle,color='blue')
Output
Consider the above nested loop, which exhibits Static Control Part (SCOP) characteristics, the iteration vectors we get are as follows:
{(1, 2),(1, 3),(1, 4),(1, 5),(1, 6),(1, 7),(1, 8),(1, 9),(2, 3),(2, 4),(2, 5),(2, 6),(2, 7),(2, 8),(2, 9),(3, 4),(3, 5),(3, 6),(3, 7),(3, 8),(3, 9),(4, 5),(4, 6),(4, 7),(4, 8),(4, 9),(5, 6),(5, 7),(5, 8),(5, 9),(6, 7),(6, 8),(6, 9),(7, 8),(7, 9),(8, 9)}.
These vectors correspond to the values of the i and j variables within the loop bounds.
And the vectors satisfy loop-bound conditions; 1<= i < 9 and i+1 <= j < 10
From loop bound condition we derive the Presburger formula; i >= 1 ∧ i < 9 ∧ j > i ∧ j <= 9
Thus, we can say the iteration vectors also satisfy the Presburger formula. As a result, this set of iteration vectors can be called a Presburger Set.
The Presburger formula and set can be expressed in set builder notation as; {S[i,j] : 0 < i < j <= 9}
This notation can be passed as an argument to isl.BasicSet, and we can visualize the iter domain derived from the set (refer to the output diagram above).
So my doubts are…
Q1. Are the connections that I have explored on the right track?
Q2. If the answer to Q1 is NO, what am I missing?
N.B.: I am aware that my explorations so far may be somewhat abstract, but I would greatly appreciate insights into whether I am misunderstanding anything.
Thank you