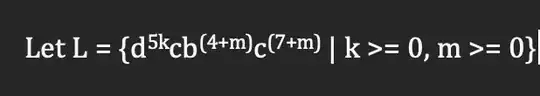So this is the language that I need to prove is irregular via pumping lemma, however I am completely stuck with this and seeking some advice. The other ones I have done during my tutorial are much more simple but struggling a bit more when it comes to having two conditions as such. Any help would be appreciated
Suppose towards a contradiction that $L$ is regular and let $p$ be its pumping length. Consider the word $w = cb^{4+p}c^{7+p} \in L$. By the pumping lemma, $w$ can be written as $xyz$ with $|xy| \le p$ and non-empty $y$ such that $xy^iz \in L$ for all $i \ge 0$.
By our choice of $w$ either $y = cb^k$ for some non-negative $k < p$ or $y=b^k$ for some positive $k$. In the former case $x=\varepsilon$ and $xy^0z = z \not\in L$ (to see this, notice that $z$ starts with neither $c$ nor $d$). In the latter case $xy^0z = cb^{4+p-k}y^{7+p} \not\in L$.
Since we reach a contradiction in both cases, we conclude that $L$ cannot be regular.
Alternatively (as per you comment) you can "pump" $w$ as follows. In the former case, $xy^2z$ starts with $cb^kcb^k$, hence $xy^2z \not\in L$. In the latter case $xy^2b = cb^{4+p+k}y^{7+p} \not \in L$ (since $k \ge 1$).
Assume you parsed c b^(m+4) for some m. Show that different m must give different states.
You are in a state where c^(m+7) leads to an accepting state. After parsing c b^(m’+4) for m’ ≠ m the same input does not lead to an accepting state, so you are in a different state. Since there are infinitely many different m a finite state machine cannot parse the language.
