Say that I have a plasma gun:
It's easy to compute the trajectory of the plasma ray starting from the gun.
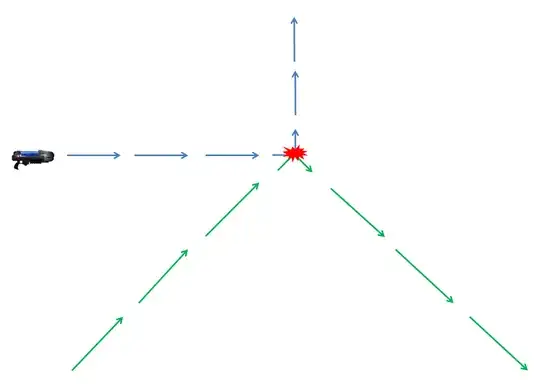
However, another ray may come from afar:
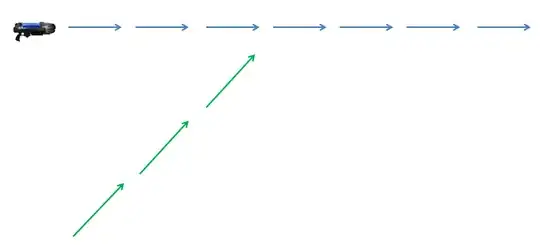
As everybody knows, plasma rays are deviated when they collide. In fact, they are always deviated 90°, away from the other ray:
Space is discreet (like a chess board). Each tile may contain either a plasma gun, a plasma ray or nothing. Rays can go either straight or diagonally. An important precision: rays are "instant", they do not take any time to propagate.
I need to compute a "solution" trajectory for all rays that satisfies all constraints.
I can easily compute a ray propagation step by step, but if a collision is detected with other ray, it seems that I will need to "backtrack" that ray up to the point of collision, to then restart propagating it correctly.
Any suggestion of an algorithm to do this? Maybe lists are not really indicated for this, and I should use graphs (nodes being collisions)?
I would be also glad if you point me to some class of similar algorithms/research... Thanks!
EDIT:
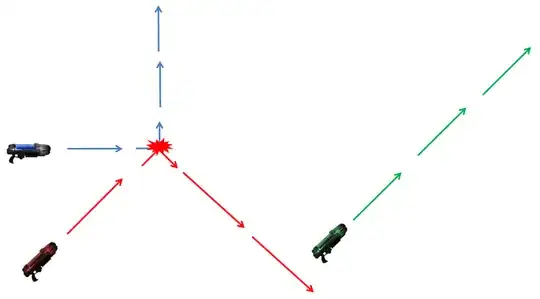
Note that collisions can have cascading consequences.
For example in this situation:
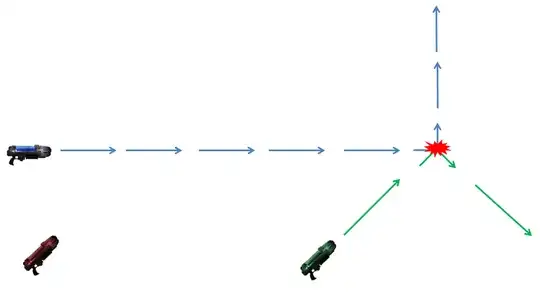
If I fire the red plasma gun, This is what I should get:
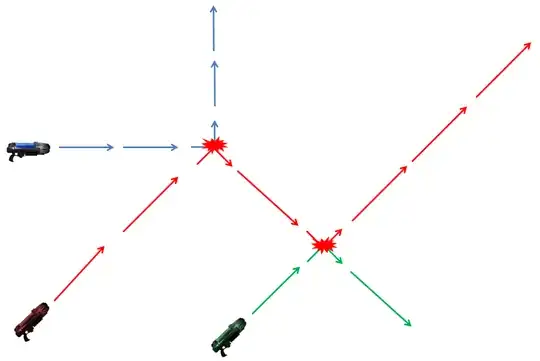
The green trajectory was affected by the new collision between red and blue. New collisions can also appear:
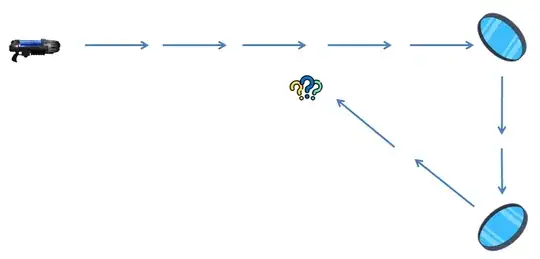
Last but not least, paradoxes can appear: