3

In the dragon book, section 9.2.6, why is the $OUT[B]$ initialized to $U$ except for $OUT[ENTRY]$. Wouldn't using the $OUT[B] = \emptyset \quad \forall B$ be a more conservative solution? The book gives this example:

enter image description here

Let $IN[B_2] = OUT[B_1] \cap OUT[B_2]$

$OUT[B_2] = G \cup (IN[B_2] - K)$

and $I^j, O^j$ be the $j$th approximations of $IN[B_2]$. Namely,

$I^{j+1} = OUT[B_1] \cap O^j$

$O^{j+1} = G \cup (I^{j+1} - K)$

The book argues that 1st approximation of $IN[B_2]$, $I^1$, is

$I^1 = OUT[B_1] \cap OUT[B_2] = OUT[B_1] \cap O^0 = OUT[B_1] \cap U = OUT[B_1]$

more "desirable". I don't see why we cannot initialize $OUT[B] = \emptyset \quad \forall B$ since based on the two dataflow equations above:

\begin{align} I^1 &= OUT[B_1] \cap O^0 \\ &= OUT[B_1] \cap \emptyset \\ &= \emptyset \end{align}

\begin{align} O^1 &= G \cup (I^1 - K) \\ &= G \cup (\emptyset - K)\\ &= G \end{align}

\begin{align} I^2 &= OUT[B_1] \cap O^1 \\ &= OUT[B_1] \cap G \\ \end{align}

This seems to be more intuitive to me, it says "the set of expressions available on entry into $B_2$ are those that are generated by $B_1$ and $B_2$" which seems on the right track. If any expression made available in $B_1$ is killed in $B_2$, $O^2$ will quickly fix this,

\begin{align} O^2 &= G \cup (I^2 - K) \\ &= G \cup ((OUT[B_1] \cap G) - K) \end{align}

So my questions really are:

  1. Does initializing $OUT[B] = \emptyset$ ever produce an incorrect analysis? In other words, when the Maximum Fixed Point algorithm terminates, is there a case where the set of available expressions is not a subset of the truly available expressions?

  2. Assuming #1 does indeed produce a correct analysis, is the set of available expressions found using the $\emptyset$ initialization the same as those found using the $U$ initialization? If not, why is one larger than the other?

David Yue
  • 133
  • 4

1 Answers1

2

I had a similar question. I think the conclusion is that starting with the empty set will give you a valid solution, but it won't always be the largest possible solution. We desire the largest possible solution so that we can eliminate as many common subexpressions as possible and therefore optimise the generated code as much as possible.

Does initializing OUT[B]=$∅$ ever produce an incorrect analysis? In other words, when the Maximum Fixed Point algorithm terminates, is there a case where the set of available expressions is not a subset of the truly available expressions?

I think it won't produce an incorrect analysis. Assuming these equations are implemented in the algorithm described in the book, whereby you iterate until changes to the OUT sets stop occurring, it's impossible for the loop to terminate with IN and OUT values that do not satisfy the equations. This is because the loop terminates exactly when for all B, OUT[B] before the loop equals the value of OUT[B] predicted by the equations. If the equations are not satisfied the loop can't have terminated because there's a discrepancy between the LHS and RHS, which would cause an update in the iterative algorithm.

I think it's helpful to see the derivation of the algorithm in 2 parts. First they specify the equations which define the problem, then they give an algorithm to solve these equations iteratively. Our $∅$ proposal only modifies the algorithm, so the mapping between a solution to the equations and a valid analysis is not impacted. Since (as argued in the above paragraph) we still get a valid solution to the equations, we will have a valid available expressions analysis. [See slide 50 here https://www.cl.cam.ac.uk/teaching/1718/OptComp/slides/lecture04.pdf which claims that "any solution ... is safe"]

However, there is a question about whether starting with $∅$ can prevent the algorithm from terminating. I think the algorithm must still terminate because essentially you can argue that once an expression has been added to the OUT set of a given block, it can't be removed because that would require it to have been removed from a predecessor's OUT set, which requires it to have been removed from a predecessor's OUT set etc recursively with no base case. Normally when you start with U it is possible to remove stuff because the kill sets cause removals, but effectively when you start with $∅$ the kill sets have already been processed and remain constant.

Assuming #1 does indeed produce a correct analysis, is the set of available expressions found using the $∅$ initialization the same as those found using the U initialization? If not, why is one larger than the other?

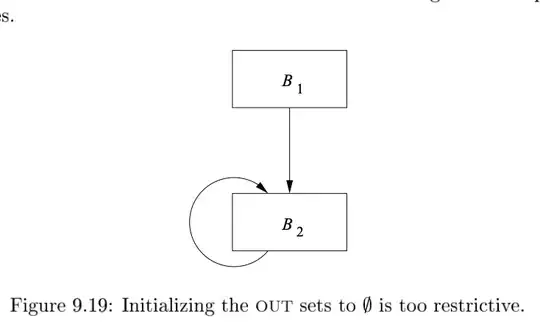
Then, as you highlight, the question is: why should we want to choose $U$ over $∅$? I think an example of why it matters in this case is if G is the empty set. In that case $O^1 = G = ∅$ and the algorithm terminates since there haven't been any changes to any OUT values in the first iteration. So, in that case, the analysis concludes with a solution OUT[B2] = $∅$. But, the 'complete' solution is OUT[B2] = OUT[B1] because B2 is only ever preceded by B1. Using the $∅$ initialisation would cause us to not realise that expressions computed in B1 are available in B2. The fact that B2 doesn't generate any expressions shouldn't block it from using expressions generated in B1.

I assume that the authors selected this example because it's a small program to make it easier to explain. The impact of having a smaller-than-necessary set for B2 is seemingly innocuous here because the program is small but I guess in bigger programs we could deviate quite substantially from the maximal solution, missing many opportunities for optimisation.

Hamish Starling
  • 36
  • 4