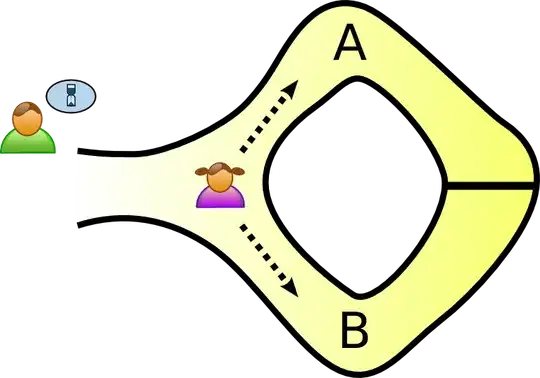
"The Ali Baba cave" example of ZKP is pictured below. There is no need for a probabilistic ZKP protocol to prove to the verifier of the statement (that the prover has the key to the door). It can be proved deterministically without the prover revealing any knowledge/information.
Assume that both the verifier and prover are both initially positioned at one side of the door. The verifier first walks back to the entrance. The prover opens the door and walks to the entrance to meet the verifier using the opposite route that the verifier took. Hence the prover proves to the verifier deterministically, without the need for repeated experiments.