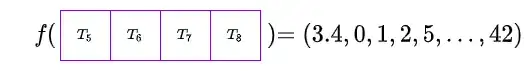Suppose we have a sequence of $m$ tokens $(T_1, T_2, \ldots, T_m)$. We can split this sequence considering two parameters $w$ (which is the width of the window) and $x$ which is the overlap between windows. This is depicted in the following figure:
Now, suppose we have the function $f$ which takes as input a window and maps it into an $\mathbb{R}^N$ vector space:
This procedure is performed for all windows of a given sequence, based on parameters $w$ and $x$. In the end, I will have a cluster of points with a centroid:
Suppose that I want to find the windows that best represents the main structure of the original sequence (based on the mapping of the function $f$), then this can be thought as an optimization problem such that getting the minimum average distance between points and the centroid (I will omit the constant $\frac{1}{n}$)
$$\text{Minimize } J(w, x) = \displaystyle \sum_{k=1}^{n} \|v - x_k\| $$
$v$ is the centroid computed from the $n$ vectors obtained previously. The problem is that $n$ depends on $w$ and $x$
Subject to:
$$0 < w < |T|$$ $$w > x$$
$f$ could be any function, but in my case the $f$ I am using has the following properties:
- If we have window $S_1$ and a window $S_2$ such that $|S_1| \lt |S_2|$, then $\|f(S_1)\|_2 < \|f(S_2)\|_2$
- All components of the vectors resulting from $f(S)$ are greater or equal than zero.
I would like to find $w_{opt}$ and $x_{opt}$.
- In summary, the input is the sequence $T$
- Based on parameters $w$, $x$ and a mapping function $f$ we create a cluster of points.
- I'd like to find $w_{opt}$ and $x_{opt}$ for a given $f$ such that $J(w, x) = \displaystyle \sum_{k=1}^{n} \|v - x_k\|$ is minimum.
I already tried to do this with a brute force approach but it is infeasible with the sizes I am getting for the main sequence (around 300-800 tokens)