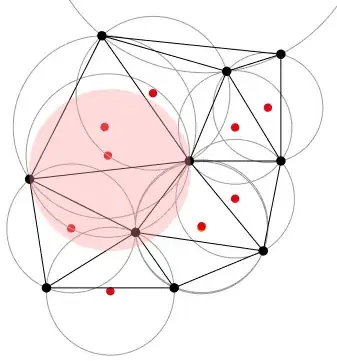
It is know that the Gabriel graph of a point set $P \subset \mathbb{R}^2$, $\mathcal{GG}(P)$ is a subset of the corresponding Delauney graph $\mathcal{DG}(P)$, i.e. $\mathcal{GG}(P) \subseteq\mathcal{DG}(P)$.
A Gabriel graph is defined as:
The Gabriel graph $\mathcal{GG}(P)$ of a point set $P \subset \mathbb{R}^2$ is defined as follows. The vertex set is $P$ and two vertices $p, q$ in $P$ are connected by an edge if and only if the interior of the disk with diameter $\overline{pq}$ is empty and $p, q$ are the only two points on its boundary. In particular, this implies that $\overline{pq}$ is also an edge in the Delaunay graph of P.
However, I am struggling to visualize or understand in what cases an edge $(p, q)$ would be in $\mathcal{DG}(P)$ but not in $\mathcal{GG}(P)$. Could someone give me an example? It seems to me as, by the empty-circle property of Voronoi edges, and their duality with the Delaunay graph, every edge in the Delaunay graph should satisfy the definition of a Gabriel graph. It is obvious that I am missing some edge case.