Is doing BFS over transitive reduction of a directed acyclic graph equivalent to topological ordering of that graph?

Question

I have a directed acyclic graph. Where each node is a task and each edge denotes a dependency.

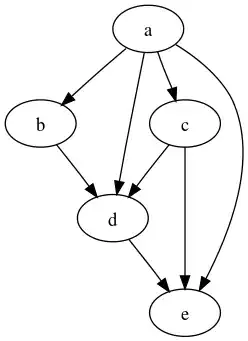
I want a method to effectively parallelize these tasks. One way would be to topological sort them based on depth. Node a which has no precedents will have depth 0. For other nodes, depth will be the depth of precedent with the highest depth +1. Like in the answer provided in this stack exchange question. But here I am not sure if we can get the most amount of parallelization. Tasks in each depth can be run in parallel. But to start processing tasks in a particular depth. All tasks in previous depth should be completed.

Then I came across the idea of transitive reduction of a DAG.

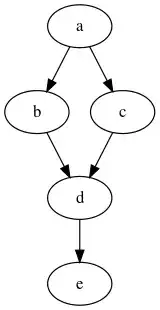
Transitive reduction reduces extra edges such that the same reach-ability relation in the original graph is maintained. Does this mean that transitive reduction is implicitly topological sorted? Does doing bfs over a transitively reduced task graph and executing tasks as they come in the bfs order equivalent to topological order?. For the input graph and its transitive reduced version, they seem equivalent. I don't know if there are any cases I am missing. What I want is a way to parallelize a task graph with maximum throughput.

Answer 1

Yes, using the approach you sketched based on topological sorting gives you the maximum throughput, assuming you have an unlimited number of processes (there is no limit on the number of tasks you can solve in parallel).