Why does the Huffman coding algorithm produce a valid tree?

Question

I am not asking about the Huffman Code, but the most widely described algorithm for generating one, also described on the english wikipedia: https://en.wikipedia.org/wiki/Huffman_coding#Compression

Now, I am not really concerned with the code being optimal or not, because many proofs for this can be found, but there is one thing that bothers me - why can I be sure, that for any path on the Huffman Code tree, no string constructed from labels is a prefix of another string in the tree?

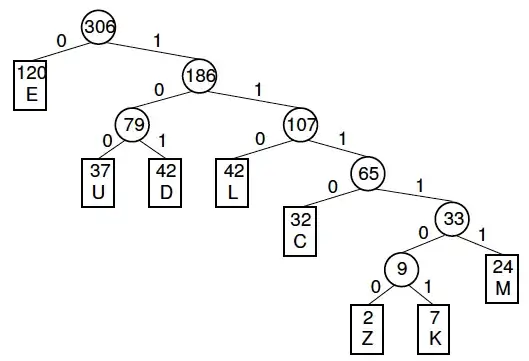
Considering a simple tree (source: http://homes.sice.indiana.edu/yye/lab/teaching/spring2014-C343/huffman.php):

It has these codes: E - 0 U - 10 D - 01 L - 110 C - 1110 M - 11111 Z - 11110 K - 11111,
and it is obvious, that none of these codes is a prefix of another. However, I am looking for a general proof that this is true for any Huffman tree, which for some reason I am unable to find. I would be grateful for any sources.

Answer 1

Let $v$ be a vertex of the tree. If $\pi_v$ is the path from the root of the tree to $v$, then the string $s(v)$ constructed from the labels of $\pi_v$ is unique (if you really want, you can prove this by induction on the depth of $v$).

If $s'$ is a proper prefix of $s(v)$ then there is a node $u$ in $\pi_v$ such that $s(u)=s'$ and, by the above observation, this node is unique. Moreover, $u$ cannot be a leaf (since it precedes $v$ in $\pi_v$).

This means that, for each leaf $v$ there is no prefix of $s(v)$ that matches the code $s(v')$ of another leaf $v'$. Since the symbols only appear as leaves of the tree, this means that the code is not ambiguous.