How to use DFA/NFA to prove the language {$0^n 1^$ | x ∈ Σ*, n ≥ 1} is regular?

Question

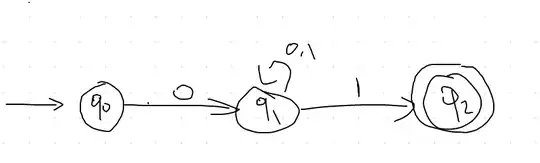
I'm trying to prove the language L = {$0^n 1^$ | x ∈ Σ*, n ≥ 1} is regular, but don't know how to present it in a DFA/NFA. I'm thinking to have n+1 states in a NFA, with the start state as the accepting state. The NFA reada $0$s to go from q$0$ to q$n+1$, then reading $1$s or $0$s to stay in the q$n+1$, then reading the same number of $1$s to go back to the q$0$. Is this a valid way to prove L is regular?

Answer 1

Your language consists of all words starting with $0$ and ending with $1$.

Answer 2

Your solution depends on $n$. In this case the $n$ in the formulation of the language is not a constant, but a variable ranging over the positive integers $n\ge 1$. So we need strings of the form $0^n x 1^n$ for any $n\ge 1$, and any $x\in\Sigma^*$.

In general that would not be possible with a FSA, it cannot count and compare the numbers of $0$'s and $1$'s, but this is a trick question. See the answer by Yuval.

Answer 3

Your language is regular and can be rewritten as $$ L = {0\Sigma^*1} $$ (start with 0 end with 1)