Sort half-edges around common vertex in 3d

Question

I'm trying to figure out this problem for very long time and am no getting nowhere. I'm working on a simple 3d modeler that uses half-edge data structure.

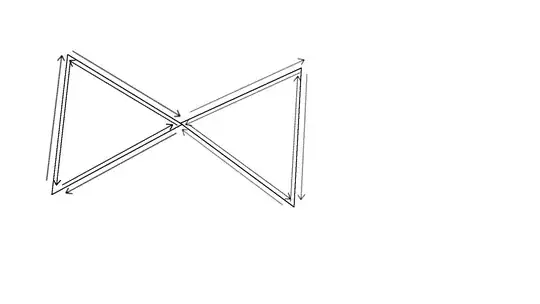
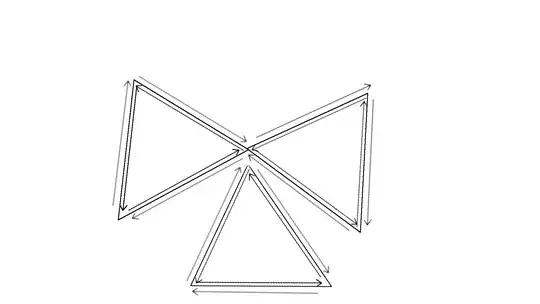
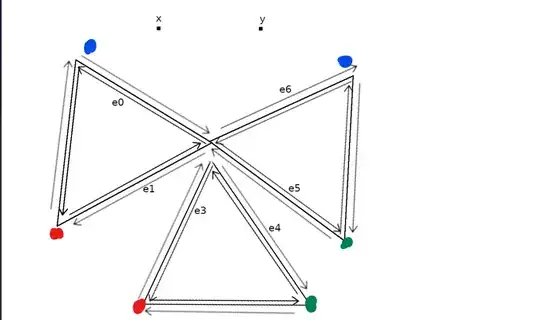
Say I have non-manifold geometry where two triangles share a common vertex, as shown in the image below. And I want to add another triangle such that now three triangles share a common vertex. Once we add the new triangle we need to reorder the half-edges around the common vertex. In 2d this ordering is done by sorting the half-edges from the common vertex clockwise, as explained in this post.

However in 3d this becomes a nightmare. If the same three triangles share the common vertex but have an arbitrary orientation in 3d space and are not coplanar. How can one possibly sort the half-edges?

I experimented with using the common vertex normal to construct a plane, and project all the half-edges around the vertex to that plane. After which we could sort them clockwise relative to the plane. But I've found this approach to have a lot of issues. And now I'm all out of ideas.

Answer 1

It seems that the problem here is that you try to determine something similar to a rotation system from a skeleton¹ embedded in $\mathbb{R}^3$. The problem here is that such a skeleton is not enough to uniquely define a rotation system, because rotation systems encode embeddings of a graph onto a surface. Without having access to a given surface as a reference, almost any rotation along a vertex is possible, and you will not be able to find the "right" one.

So what can you do? This likely depends a bit on what it is you are actually modelling. Since the rotation around a vertex is a concept that depends on a surface, to determine it you will have to decide what your surface looks like, at least locally around the vertex you're inserting a triangle in. Likely, the edges that are part of a triangle should always be consecutive in the ordering, but that doesn't give all the information.

One possible approach on how to decide where a new triangle fits into the ordering, is to look at all consecutive pairs of triangles in the existing ordering, and insert the new triangle in between the pair with smallest distance to the new triangle. (Note that you have to store the ordering around the vertex explicitly, you cannot compute this on the fly)

More precisely, to determine where to place a new triangle incident to vertex $v$ in the ordering around $v$, consider all pairs of consecutive edges $(e_i,e_{i+1})$ that do not form a triangle with vertices $(a,b)$ being their endpoints not equal to $v$. Let $(x,y)$ be the new vertices of the triangle. Place the edges of the new triangle in between the pair of edges $(e_i,e_{i+1})$ such that $\min(\|a-x\|+\|b-y\|, \|a-y\|+\|b-x\|)$ (or another similarity measure of the pairs $(x,y)$ and $(a,b)$) is minimized.

For example, in the figure below, vertices with the same colors are the pairs we'd compare with our new vertices $x,y$.

---

_{1: I will assume that you just have a graph for now, but perhaps a simplicial complex might be a better description? I don't think it matters much for the discussion here, though.}