Managing an hotel using AVL trees - Data Structures

Question

I have a Data Structure question where I need to manage an hotel, each room has a number between $1-n$
and it can be occupied or not.

Available Data structures: AVL* Trees, B-Trees, Arrays, Stacks, Queues, Binary Trees.

$O(n)$ Space complexity available.

Using AVL OR B-Tree is a must.

I have to support these functions:

1) $\text{Init(n)}$ : Initializes the data structure with $n$ unoccupied rooms, the indexing of the rooms is $1-n$
this has to work at $O(n)$ time complexity

For the next functions: $l$ and $r$ do not have to be a number of an occupied room-

2) $\text{GetUnOcc(l,r)}$ : Gets $l$ -Left and $r$ - Right (Does not have to be an occupied room number) , 2 numbers that defined a range of numbers and I need to count how many hotel rooms are not occupied between them (Including). Has to work at $O(\log_2{n})$ Time complexity

3) $\text{GetMinUnOcc(l,r})$ : Gets $l$-Left and $r$-Right, 2 numbers that define a range of numbers, this one adds the person to the hotel at the smallest room that is not yet occupied between $l-r$ (Including).
Has to work at $O(\log_2{n})$ Time complexity

4) $\text{GetOut(r)}$ : It gets a room number and deletes the person from that Room/Hotel, making room number $r$ unoccupied.
Has to work at $O(\log_2{n})$ Time complexity

My Go:

Init: I thought about using an AVL tree with a boolean array.
We initialize it $O(n)$ by just making an array of False (Unoccupied) which takes $O(n)$

GetUnOcc(l,r) : I thought about this formula:
$\text{#UnOcc} = r - l + 1 - \text{Occupied}$ so we need to find how many rooms are occupied between $l-r$ but I am not sure how to do so in $O(\log_2{n})$

GetMinUnOcc is much harder because I cannot determine which value is the smallest, let's say $l=3$ and $r=10$ and every room between $3-8$ and room $10$ are occupied, and I need to return $9$ (because it is the smallest which is not occupied)

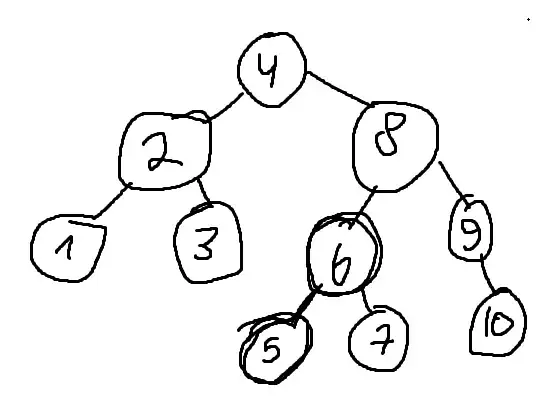
Let's say I have this tree (as Steven suggested to build an AVL of unoccupied rooms) so in this matter it is $\text{Init(10)}$ And Now I want to do $\text{GetMinUnOcc(5,7)}$ so it should delete $5$ from the tree as it will become occupied. But in what you suggest, we find the successor of $l=5$ which is his parent, $6$ and delete it, but, $5$ is not occupied and we want to return the minimum so we need to actually delete $5$, where am I wrong? Thank you!

I would appreciate your help / hints to solve this hard question! Thank you!

Answer 1

Maintain an AVL tree $T$ containing the indices of the unoccupied rooms. For each vertex $v$ of the tree additionally maintain the number $\eta(v)$ of vertices in the subtree of $T$ rooted at $v$.

1) Init: create an AVL tree with keys $\{1, \dots, n\}$. This requires $O(n)$ time.

2) GetUnOcc($l$, $r$): Find the vertex $u$ associated with the successor of $l$ in $T$ (possibly $l$ itself). Find the vertex $v$ associated with the predecessor of $r$ in $T$ (possibly $r$ itself). If the key of $u$ is larger than the key of $v$ return $0$. Otherwise find the least common ancestor $w$ of $l$ and $r$. Initialize the number $x$ of unoccupied rooms to $0$. Walk from $u$ (inclusive) to $w$ (exclusive). Whenever you encounter a vertex $z$ such that $z=u$ or the previous vertex in the walk was the left child of $z$, let $z'$ be the right child of $z$ (if any) and add $1 + \eta(z')$ to $x$ (if $z'$ does not exist then add $1$ to $x$). Walk from $v$ (inclusive) to $w$ (exclusive). Whenever you encounter a vertex $z$ such that $z=v$ or the previous vertex in the walk was the right child of $z$, let $z'$ be the left child of $z$ (if any) and add $1 + \eta(z')$ to $x$ (if $z'$ does not exist then add $1$ to $x$). Return $1+x$.

3) GetMinUnOcc($l$, $r$): Search for the vertex $u$ associated with the successor of $l$ in $T$ (where the successor of $l$ might be $l$ itself). If the key of $u$ is at most $r$, delete $u$ from the tree subtract $1$ from the values $\eta(z)$ of all proper ancestors $z$ of $u$. Otherwise all rooms between $l$ and $r$ are already occupied.

4) GetOut(r): Insert a new vertex $z$ with key $r$ into the tree with $\eta(z)=1$. Increment by $1$ the values $\eta(z')$ of all the proper ancestors $z'$ of $z$.

Answer 2

This can be done using a simple array.

Note that the complexity depends on the total number of rooms, and not on the number of (un)occupied rooms. So we might as well store all rooms. The trick to do the counting of free rooms is basically the same as in the case of AVL trees in the other answer. On top of the linear list of arraus we build a complete binary tree, such that each node stores the number of free rooms in the interval of rooms below.

We can find the number of free rooms in an interval by looking for the rooms $\ell$ and $r$ in the tree, and start counting from the node where the two paths diverge. Then for $\ell$ we count the free rooms to the right, for $r$ the free rooms to the left.

The next free room from position $\ell$ is found as follows. First go up in the tree untill we find a node where we came from left, and the right subtree has an unuccupied room. Then go down to the first free spot.

Going up and down, left and right is done using bit-matic. I strore the rooms in the odd indices. The ndes above are even. The number of trailing zeroes in the binary index indicates the level of the node. Left nodes end with "01" and then zeroes, right nodes have "11" and zeroes.

Picture below depicts eight rooms, stored at positions 1,3,5,...,13,15. Numbers in the tree indicate free rooms. So in this situation leaves 3,5,9,11,15 are occupied, indicating rooms 2,3,5,6 and 8.

Storing the complete tree as an array is also done for binary heaps. However, the representation is different. For the heap the root is the first node in the array. Kind of upside down from this one.