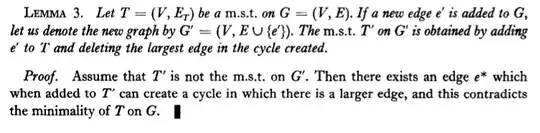MST - algorithm to add an edge to the graph

Question

I have some difficulty proving the correctness of my solution to the following exercise. Let $G = (V,E)$ undirected connected graph, $w \colon E \to \mathbb{R}$ weight function. Let $T$ a MST (minimum spanning tree) of $G$. Now, we add a new edge $e'$ to $E$ with weight $w(e')$. Find an algorithm that updates $T$ so it will be a MST of the new graph $G' = (V,E \cup \{e'\})$. The time complexity of the algorithm should be $O(V+E)$.

Intuitively, the algorithm is quite simple: add $e'$ to $T$, and then we got one cycle closed. Remove the edge with maximal weight from this cycle, and obtain a MST of $G'$.

However, I had some difficulties prove the correctness of this algorithm formally, and would appriciate some help.

BTW. I have read this post: If I have an MST, and I add any edge to create a cycle, will removing the heaviest edge from that cycle result in an MST? but unfortunately haven't fully got the proof there.

Update: I tried Steven's solution and it helped me a lot, thanks again. I also found this solution online (I add a picture), but didn't understand it well. I also don't understand why in this solution, $T'$ is the MST on $G'$ instead of a MST on $G'$. Can someone help me understand what is going on the proof there, please?

Answer 1

Let $T$ be the MST of the original graph $G$ and let $e'$ be the newly added edge. Suppose for simplicity that all edge weights are unique (if they are not, fix any arbitrary linear order among $E(G)$ that prioritizes the edges in $E(T)$. Then break weight ties according to this order).

Let $e$ be the edge of maximum weight in the unique cycle $C$ of $T + e'$. And assume that $e \neq e'$ (otherwise the proof is trivial).

One way to prove that $T-e+e'$ is a MST of $G+e'$ is showing that no edge $f \in \{e\} \cup E(G) \setminus E(T)$ can belong to any MST of $G+e'$ using the cycle rule.

If $f=e$, $f$ cannot belong to any MST of $G + e'$ because it is the edge of maximum weight of the cycle $C \subseteq T+e' \subseteq G + e'$.

If $f \in E(G) \setminus E(T)$ then, since $f \not\in E(T)$, $f$ must be the edge of maximum weight of some cycle $C' \subseteq G \subset G + e'$ and hence it cannot belong to any MST of $G + e'$.