Converting an NFA to regex using GNFA algorithm?

Question

So I've been trying to crack this for a long time and almost feel like I am going in loops about this question.

Given the following NFA:

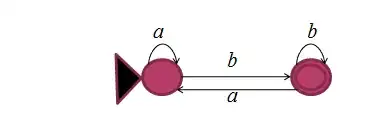
Using the GNFA algorithm get the regular expression.

I understand that you would have the following for the first step(adding empty states):

The next step would be removing the state [q1] I would get:

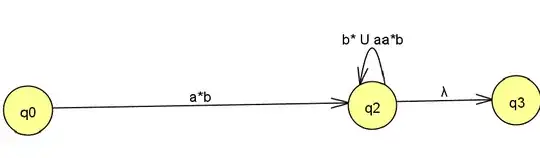
Finally removing [q2] would get:

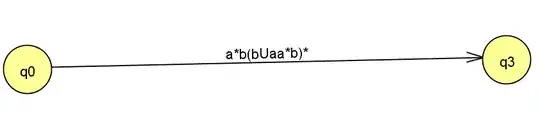
However the answers others have got is: $(a \cup bb^*a)^*bb^*$ Which does not make sense as I got, $a^*b(b \cup aa^*b)^*$? A GNFA(generalised nondeterministic finite automaton) is described as follows:

A GNFA is similar to an NFA but must obey certain rules:

• It has only one accept state
• The initial state has no transitions coming into it
• The accept state has no transitions coming out from it
• A transition can denote any regular expression, rather than just a symbol from the alphabet Note that a symbol is a kind of regular expression.

Furthermore, We may convert an NFA into a GNFA as follows:

• Add a new start state with an ε-transition to the old start state
• Add a new accept state with ε-transitions from the old accept states
• If arrows have multiple labels, or if there are multiple arrows between two states, replace them with the union (or) of those labels

Answer 1

Do you want to know why "the others" obtained a different expression?

When constructing a regular expression, there is no unique correct answer. There are usually several expressions "that make sense." In this case, you use the state elimination method (I learned this under the name of Brzozowski and McCluskey). Here, the order of removal determines the expression found. So, what do you get when removing $q2$ first?

You can also do "clever tricks" during the construction. In your example, you have $b\cup aa^*b$, which is equivalent to $a^*b$.