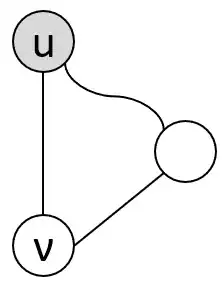
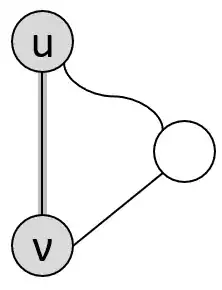
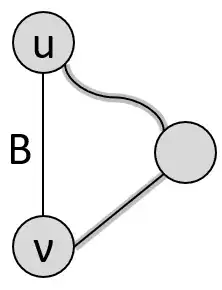
Prove that if G is an undirected connected graph, then each of its edges is either in the depth-first search tree or is a back edge.
Now, from intuition and in class lectures by Steven Skiena, I know that the above holds true, since it dives all the way down, and then throw a rope back to a previous vertex. I also know that DFS is great in finding cycles.
However, my problem here is that I don't know how to prove that the edge is either a tree edge or a back edge.
A depth first search on a directed graph can yield 4 types of edges; tree, forward, back and cross edges. As we are looking at undirected graphs, it should be obvious that forward and back edges are the same thing, so the only things left to deal with are cross edges.
A cross edge in a graph is an edge that goes from a vertex $v$ to another vertex $u$ such that $u$ is neither an ancestor nor descendant of $v$. So what you need to argue is that in an undirected graph, there's no way you can get a cross edge. It might help to think of why the can occur in directed graphs, and why you can't have this case in undirected graphs.
Let $G=(V,E)$ to be a graph and $u$ and $\nu$ to be its vertices such that $\{u,v\}\subseteq V$ and $(u,\nu)\in E$.
Suppose that $u$ is discovered first. Consequently, its color is changed to gray. Then, $\nu$ becomes its descendant (by white path theorem) and the following discovery time relationship holds: $u.d<\nu.d$.
Now, there are two options of discovering $(u,\nu)$ edge:
$\quad$ 1) if $u$ discovers $\nu$, then $(u,\nu)$ is a tree edge;
$\quad$ 2) if $\nu$ discovers $u$, then $(u,\nu)$ is a back edge since $u$ is still gray at the time the edge is first explored.
The most voting answer says well and I want to claim it more clearly.
Proof:
We know that DFS produces tree edge, forward edge, back edge and cross edge. Let's prove why forward edge and cross edge can't exist for DFS on undirected Graph.
For forward edge (u, v):
Forward edge is said that v is a descendent of u, or we say v is visited and explored completely when u is being exploring, which is
(pre[u] < pre[v] < post[v] < pre[u])
this answer is considered as a back edge because (v, u) is an edge as well. But I don't know why to see forward edge as a back one not the inverse insight. Maybe this thought is used for some specific usage?
For cross edge (u, v):
this is the difficulty of the proof.
We prove that DFS on undirected graph can not yield a cross edge by contradiction.
If (u, v) is a cross edge, then v is already explored completely when u is being explored.
(pre[v] < post[v] < pre[u] < post[u])
This can exist on DAG because when exploring v we don't know u at all! u points to v directedly. However, in undirected graph, when we explore v, u (as a neighbor of v) is being explored and finished. If the cross edge exists, then u can not be a neighbor of v, this contradicts with the undirected graph assumption. In this case, cross edge can not exist.
In fact, this proof gives us another property.
For an edge (u, v) in an undirected graph, if post(v) < post(u), then u must be an ancestor of v.
There's another approach here. Suppose that you have an edge $(u, v) \in E$ and $u, v \in V$. Now, assume that there's a forward edge in the direction from vertex $u$ to $v$. This edge is first explored in the direction of $(v, u)$ while $u$ is gray by scanning the adjacency list of $v$, since $v$ is a descendent of $u$. In the direction from $v$ to $u$, this edge is a back edge.
Then, in a connected undirected graph, there's at least one simple path between any pair of vertices. Therefore, each vertex is either an ancestor or a descendent of the other. Thus, no cross edges are possible.
If you are doing DFS on one child of the parent in a DIRECTED GRAPH and you visit the u node,
and then go down the heirarchy,
now when the recursive call folds back at u,
you cannot go towards v as the node is directed from v to u.
And when you visit v,
you can visit u from there
as there is a node in between.
When you visit u from there,
you know that u is already visited
and hence you call it a cross edge,
as the discovery time of u is before that of v.
But if your graph was undirected
then you could go from u to v because there would have been no direction constraint
and v would become a tree edge.
That is why a cross edge cannot exist in undirected graph.
In the undirected graph we get only tree and back edges . the reason for no forward edges is because in undirected the forward edges get converted into back edges , it is so because in undirected there is no restriction in which direction to visit the vertex, so in case we have any vertex we can visit it from the child itself to the parent which counts as a back edge.
now lets talk of cross edge here also since edges are undirected so, the cross edges get converted to the tree edges as they can be visited as and when we go to any of that edge vertex for more details you can view this MIT vedio https://youtu.be/AfSk24UTFS8?t=36
