I got stuck on this question while studying for final exam.
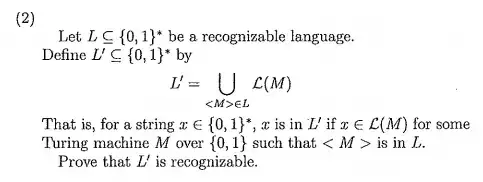
I thought about reducing L' to L to prove that L' is recognizable since L is recognizable. I am not 100% sure if that is correct.
I got stuck on this question while studying for final exam.
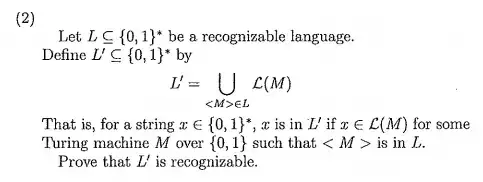
I thought about reducing L' to L to prove that L' is recognizable since L is recognizable. I am not 100% sure if that is correct.
sPaz, your answer in the comment is on the right track.
I'll give you some more hints.
The standard technique of "running in parallel" (dovetailing) should help you to complete your proof. In more details:
We have a counter $i$. We run $i$ steps of $R$ on any machine $M_j$ such that $\langle M_j \rangle < i$. We keep a list of all the machines that were accepted by $R$. For each such machine, we run $i$ steps of that machine on $x$. If any of them accepts, we accept. Otherwise, we set $i\leftarrow i+1$ and continue.