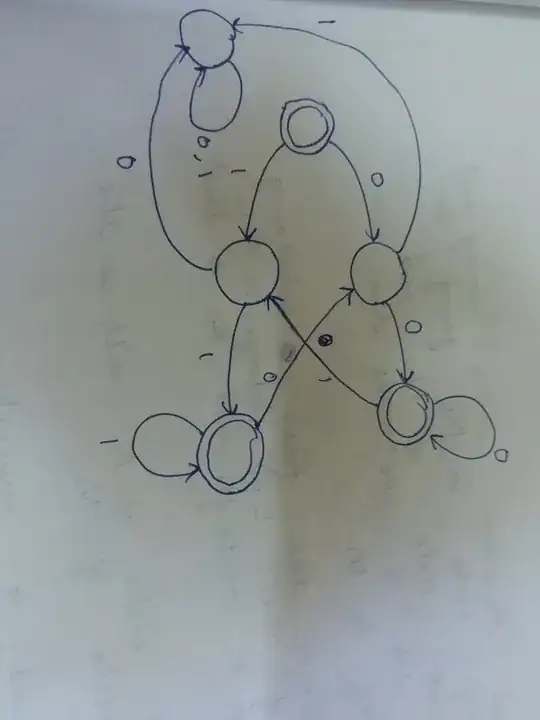
You state two questions.
(1) You are convinced that all the strings decribed by the RegEx are accepted by the DFA. In order to conclude equality you want to know the converse. Is every string accepted by the DFA also described by the RegEx? To do this, try to argue that every string accepted by the DFA consists of "blocks" of each time at least two the same letter. This is not very dificult: the states of the DFA here "count" symbols $0$ and $1$.
(2) In the title of the question you ask whether the number of states is minimal. This can be done by arguing the no states can be merged. This can be shown by giving for each pair of states a string that "distinguishes" the states: states $p$ and $q$ are distinguished if there is a string $w$ such that $w$ from one of $p$ and $q$ reaches an accepting state, while it does not reach an accepting state from the other.
Here this can be done by looking at most one letter ahead: can be reach an accepting state by $\lambda$, $0$ or $1$? For each of the six staes the answers are different.