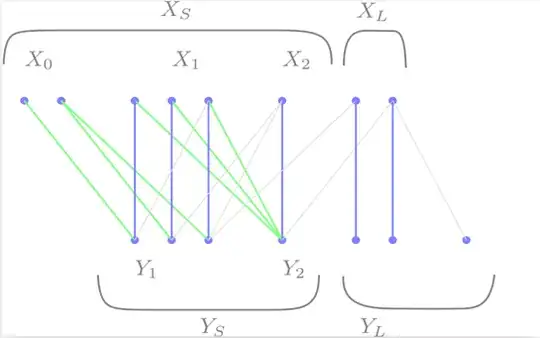
Let $M$ be a maximum cardinality matching in a bipartite graph $G(X+Y,E)$. Let $X_0$ be the subset of $X$ unmatched by $M$. Define the following sequence:
- $Y_1 = $ the neighbors of $X_0$ using edges in $E\setminus M$.
- $X_1 = $ the neighbors of $Y_1$ using edges in $M$.
- $Y_2 = $ the new neighbors of $X_1$ ("new" = not in $Y_1$) using edges in $E\setminus M$.
- etc...
Since the graph is finite, at some point we stop finding new vertices, so the process stops and we have a maximal sequence.
Let $X_S,Y_S$ be the vertices contained in the sequence, and $X_L,Y_L$ the leftover vertices:
We have a decomposition of $X$ and $Y$ into two subsets. This decompositionhas some nice properties (for example, $X_L$ and $X_S$ are the same regardless of what maximum matching $M$ we start from).
Such a nice decomposition must have a name... what is its name? And what is a standard reference for the decomposition and its properties?