Job scheduling with a bottleneck problem

Question

Given $n$ jobs $J_1,J_2,...,J_n$, each job requires $T_i > 0, T_i \in N$ time to complete.

Each job must be pre-processed and post-processed by a single machine M that can handle only 1 job at a time and both phases require 1 unit of time. After being pre-processed, job $J_i$ is sent to a machine with unlimited power (that can handle in parallel an unlimited number of jobs) and it will be ready in time $T_i$, then it must be sent (immediately) to machine M again for post-processing.

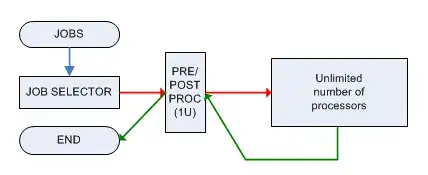
The associated decision problem is:

Input: the processing times $T_i >0, T_i \in \mathbb{N}$ of $N$ jobs, an integer $K\geq 2N$
Question: can we process all the jobs in time $\leq K$ using the above "bottleneck" model ?

Has this problem a name?
What is its complexity? (is it in $\sf{P}$ or is it $\sf{NP}$-complete?)

UPDATE 29 March:
As correctly noticed by M.Cafaro in his answer, the problem is similar to the Unconstrained Minimum Finish Time Problem (UMFT) (see Chapter 17 of Handbook of Scheduling Algorithms) which is $\sf{NP}$-hard (proved in W. Kern and W. Nawijn, "Scheduling multi-operation jobs with time lags on a single machine", University of Twente, 1993). As I can see, there are some differences because in my model:

• the pre/post processing time is constant (1 unit of time)
• as soon as the job is completed it must immediately be post-processed (the UMFT model allows delays)

I didn't found the Kern & Nawijn proof online, so I still don't know if the above restrictions change the difficulty of the problem.

Finally you can think the whole process like a single cook robot with a big oven; the robot can prepare different types of foods one at a time (all require the same time of preparation), put them in the oven, and as soon as they are cooked it must remove them from the oven and add some cold ingredients ... the "cook robot problem" :-)

Answer 1

This looks like the so called master-slave scheduling model introduced by Sahni. In particular, your problem falls under the Single-Master Master-Slave Systems. You can distinguish several cases:

1. If you do not add any additional constraint on the order of job execution (as in your case), the problem is called unconstrained minimum finish time problem (UMFT) and has been shown to be NP-hard;

2. Same Pre- and Postprocessing Orders: it is possible to design an $O(n \log n)$ algorithm to construct an order preserving minimum finish time (OPMFT) schedule;

Therefore, in case 1 your problem is $NP$-hard, while it is in $P$ in case 2.

Additional related problems are:

3. Reverse Order Postprocessing: For any given preprocessing permutation, $σ$ , it is possible to construct a reverse-order schedule, referred to as canonical reverse order schedule (CROS). Given a preprocessing permutation $σ$ , the corresponding CROS is unique. It is easy to establish that every minimum finish-time reverse order (ROMFT) schedule is a CROS.

4. no-wait-in-process constraint:

a) [MFTNW] Minimize finish time subject to the no-wait-in-process constraint; b) [OP-MFTNW] This is the order-preserving version of MFTNW. That is, minimize finish time subject to the no-wait-in-process and order-preserving constraints; c) [RO-MFTNW] Minimize finish time subject to the no-wait-in-process and reverse-order constraints.

Problems $a$ and $b$ are NP-hard, while $c$ admits a polynomial time solution.

Additional details in Handbook of Scheduling, chapter 17.

Answer 2

The question is proven NP-hard in "Minimizing Makespan in a Two-Machine Flow Shop with Delays and Unit-Time Operations is NP-Hard" by W. Yu, H. Hoogeveen, and J.K. Lenstra (2004). This is proven in section 9 of the paper:

Theorem 24. The problem of minimizing the makespan on a single machine with two unit time operations per job with arbitrary intermediate delays is strongly NP-hard.

The exact model studied here is that job $i$ consists of two operations that take unit time separated by some delay time $T_i$. The problem is strongly NP-complete both when the exact value of the delay $T_i$ is specified for each job, and when some minimum delay time is specified for each job.