Is there a strictly non-deterministic one-counter language whose complement is one-counter?

Question

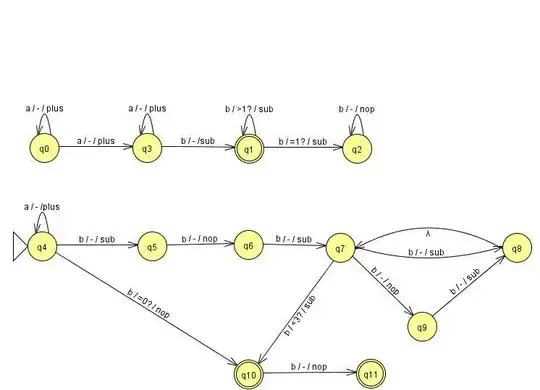
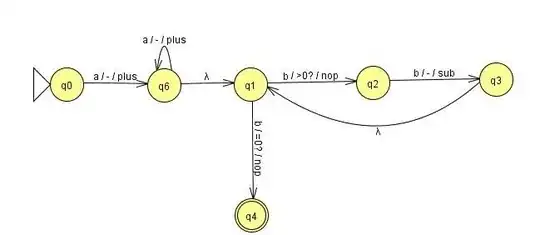
Let $A= \{L \mid L \;\text{is one-counter and \(\bar{L}\) is also one-counter} \}$

Clearly, $\text{Deterministic one-counter} \subseteq A$

Is it the case that $ A = \text{Deterministic one-counter}$?

I know that for context-free languages the analogue is not the case. For example, let $P =\{ ww^r\}$. Then both $P$ and $\bar{P}$ are context-free but $P$ is not deterministic. Hence $A$ defines a (strict) subset of the context-free languages.

The question is: can we construct a similar one-counter example for which the same holds?

Answer 1

In response to Shaull's comment above :

The first one is an image of 1-counter accepting $a^ib^j$ s.t. $j<i$

The secong one is an image of 1-counter accepting $a^ib^j$ s.t. $j>i,\ j<2i$

The third one is an image of 1-counter accepting $a^ib^j$ s.t. $j>2i$

Here a/-/plus means on seeing a, irrespective of the counter value, increment the counter. b/>1?/sub means on seeing b, if counter value is greater than 1, then decrement the counter.

nop => no operation

$\lambda $ => empty string