Floyd's Cycle detection algorithm | Determining the starting point of cycle

Question

I am seeking help understanding Floyd's cycle detection algorithm. I have gone through the explanation on wikipedia (http://en.wikipedia.org/wiki/Cycle_detection#Tortoise_and_hare)

I can see how the algorithm detects cycle in O(n) time. However, I am unable to visualise the fact that once the tortoise and hare pointers meet for the first time, the start of the cycle can be determined by moving tortoise pointer back to start and then moving both tortoise and hare one step at a time. The point where they first meet is the start of the cycle.

Can someone help by providing an explanation, hopefully different from the one on wikipedia, as I am unable to understand/visualise it?

Answer 1

You can refer to "Detecting start of a loop in singly linked list", here's an excerpt:

Distance travelled by slowPointer before meeting $= x+y$

Distance travelled by fastPointer before meeting $=(x + y + z) + y = x + 2y + z$

Since fastPointer travels with double the speed of slowPointer, and time is constant for both when both pointers reach the meeting point. So by using simple speed, time and distance relation (slowPointer traveled half the distance):

\begin{align*} 2*\operatorname{dist}(\text{slowPointer}) &= \operatorname{dist}(\text{fastPointer})\\ 2(x+y) &= x+2y+z\\ 2x+2y &= x+2y+z\\ x &= z \end{align*}

Hence by moving slowPointer to start of linked list, and making both slowPointer and fastPointer to move one node at a time, they both have same distance to cover.

They will reach at the point where the loop starts in the linked list.

Answer 2

I have seen the accepted answer as proof elsewhere too. However, while its easy to grok, it is incorrect. What it proves is

$x = z$ (which is obviously wrong, and the diagram just makes it seem plausible due to the way it is sketched).

What you really want to prove is (using the same variables as described in the diagram in the accepted answer above):

$z = x\ mod\ (y + z)$

$(y + z)$ is the loop length, $L$

so, what we want to prove is:

$z = x\ mod\ L$

Or that z is congruent to x (modulo L)

Following proof makes more sense to me:

Meeting point, $M = x + y$

$2(x + y) = M + kL$, where $k$ is some constant. Basically, distance travelled by the fast pointer is $x + y$ plus some multiple of loop length, $L$

$x + y = kL$

$x = kL - y$

The above equation proves that $x$ is the same as some multiple of loop length, $L$ minus $y$. So, if the fast pointer starts at the meeting point, $M$ or at $x + y$, then it will end up at the start of the loop.

Answer 3

Say there are $l$ elements before the loop starts and $n$ elements in the loop. And $e_l$ is the first element of the loop which is seen when we traverse the linked-list. When we will say "an element $x$ steps ahead of $e$", that will mean, we can reach that element taking $x$ steps from $e$.

Now, when Tr (tortoise) reaches $e_l$, after $l$ iterations, say, Hr (Hare) is $x$ steps ahead of $e_l$. Since Hr has taken total $2l$ steps by then ($l$ steps prior to the loop), so:

$x = l \bmod n$.

In each future iteration, Tr and Hr will progress by 1 and 2 steps respectively, and so each iteration will increase their "gap" by 1. So they will meet after $n-x$ further iterations, when their gap will become $x + (n-x) = n$. So, the meeting element $M$ will be $n-x$ steps ahead of $e_l$. Now that means, stepping $x$ steps after $M$ will again bring us to $e_l$. Our goal is to locate $e_l$.

So, when we start with one reference Tr at $M$ and another reference Hr at the head of the linked-list, and progress both of them 1 step at a time, after $l$ iterations:

• Hr will be $l$ steps ahead of the head, which is $e_l$.

• Tr will be $(l \bmod n)$ steps ahead of $M$, that is, $x$ steps ahead of $M$, which is $e_l$.

Thus when they have met, we know it is $e_l$.

See this article (written by me) for details. There you will find a slightly modified method to locate $e_l$.

Answer 4

I try to draw function curves to see what happen when two pointers velocities are not 2:1，and verified the correctness of finding the start of cycle.

https://www.desmos.com/calculator/snqtvrmhn3

Answer 5

I also think the top answer is incomplete, and while some of the other explanation are also good, I have another version without MOD to show the same thing, which is perhaps easier for some people.

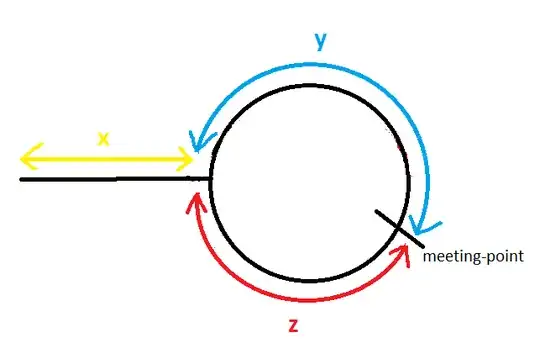
The same setup, consider $X\ge 0$ being the distance before the loop, $N \le \text{size of list}$ being the size of the loop (the quantity $y+z$ in the picture), and the meeting point be $Y$ in the Loop. At this point, notice that we have also made $X+Y \le N$.

Now, the slow pointer travels $X+Y+pN$, where $p$ is an arbitrary integer. Then fast pointer travelled $2(X+Y+pN)$.

Now, we claim that they meet at $Y$.

Proof:

If they meet at $Y$, it must be that the faster pointer travelled exactly $qN$ more than the slower pointer, where $q$ is an integer. Then we have: $$\text{distance difference = }2(X+Y+pN)-(X+Y+pN)=X+Y+pN$$. But we had $Y$ being an arbitrary meeting point in the loop, so we can choose simply $X+Y=N$, which holds as $X+Y \le N$.

Therefore, we have: $$ X+Y+pN=N+pN=(p+1)N = qN $$ which is true if $p+1=q$. Now, since both $p$ and $q$ are arbitrary integers, we can just choose the minimum so that $p=0,q=1$, which corresponds to: $$ \text{distance travelled by slow pointer}=X+Y+pN=X+Y $$ and $$ \text{distance travelled by fast pointer}=(X+Y+pN)+qN=X+Y + N $$ so the fast pointer, at the first time meeting the slow pointer, travelled exactly $N$ more.

Answer 6

Assume there are l steps to enter the loop, and the loop has length n. Using Floyd’s algorithm, tortoise and hare meet at the smallest m >= 1 where $x_m = x_{2m}$. m steps are one or more complete cycles.

If we compare $x_i$ and $x_{i+m}$ then they are the same if and only if $x_i$ is within the cycle, that is i >= l. We set tortoise = $x_0$ and hare = $x_m$ and as long as they are not the same increase them both by one step, counting the steps. They are the same for the first time when the tortoise enters the cycle, and that is after i = l steps.

PS. To find n, iterate the hare from $x_m$ until it reaches $x_m$ again after n steps. You would do that at the same time as finding the steps until the cycle. If n <= l then we find n at the same time or before l, otherwise at least we have done l steps of the search already.

PS. We know that n divides m. So if we haven’t found n after x steps where x < m is the largest divisor of m, then n = m.

PS. Brent’s loop finding algorithm usually runs faster, determines the cycle length immediately, and often knows an element $x_{m-l}$ shortly before entering the loop, makeing it faster to determine the number of steps until the loop.

Let t = h = start, m = 0
Repeat
    t = t -> next, h = h -> next -> next, m = m+1
Until t = h
Let t = start, i = 0, x = h
While t ≠ h
    t = t -> next, h = h-> next, i = i + 1
    If h = x and n unknown then n = i
l = i

Answer 7

I found the answer on stackoverflow. Thanks if anyone was looking into this for me. And for those who like me wanted an explanation, please refer to: https://stackoverflow.com/questions/3952805/proof-of-detecting-the-start-of-cycle-in-linked-list The chosen answer to the question, explains it!

Answer 8

The tortoise and the hare are two pointers that are initialized with the value of the "top" of the list. In each cycle of the loop, the hare increases by 2 incremental items, while the tortoise increases by one. If at any point, the hare equals the hare, a loop has been detected. If the hare equals the end, a loop is not found.

This post explains it better line-by-line:

https://www.thiscodeworks.com/floyd-s-cycle-detection-algorithm-aka-the-tortoise-and-the-hare-algorithms-logic-interesting/5e10a9b796432f6f7b798b29