What does that mean, that A5/1 is clocked?

Question

What does that mean, that A5/1 is clocked? What happens if the clocking bit agrees with the majority bit?

Answer 1

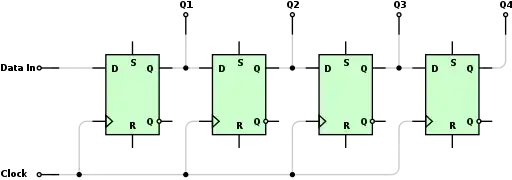
The clock term comes from electronic engineering; in each clock, the cells of LFSRs ( flip-flops) are clocked and the data moves. In the shift registers, the data moves from one to another in one direction. As we can see from the below, each flip-flop has a clock input where each has the same clock.

In the LFSRs ( Linear Feedback Shift Register) there is also the feedback that is calculated from the selected tap point is fed the beginning.

Normally LFSR's are clocked for each clock so that new feedback is calculated and the LFSR is shifted so that new output is formed. If you don't clock, then no new feedback is calculated and no shifting occurs, too. The old output is still active. To achieve this in electronics the clock is also controlled by logic. In programing that is way easier (see bottom).

Consider the first LFSR ( index names are free to choose and it is reflected)

When clocked it will become;

See that the data of the cells are shifted to the right and the new value to the left is feedback values calculated from the active taps.

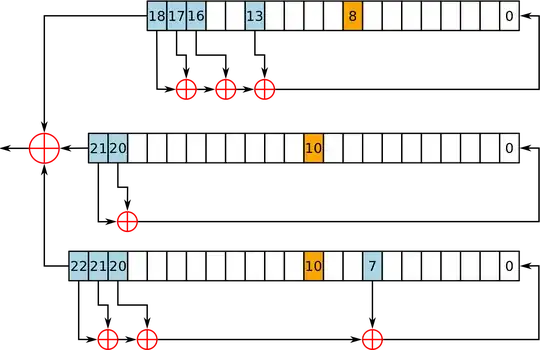
A5/1, which is terribly broken, has three LFSR where each of them has clocking bits, (8,10,10) shown orange on Wikipedia's image. At each clock, the majority is formed from those values.

The majority of the $n$ binary variable means the most occurring value. For three bits, just count the number of ones $c$ if $c > 1$ then the majority is *one ( i.e. number of ones > number of zeros) and the majority bit is $1$, otherwise the majority bit is $0$.

If the majority bit matches the LFSR's clocking bit, then the LFSR is clocked otherwise not clocked.

A simple code can be described for each LFSR as

majority = (L1[8] AND L2[10]) xor (L1[8] AND L3[10]) XOR (L2[10] AND L3[10])
def clockLFSR1(majority):
    if L[8] == majority:
        self.applyClock()
def clockLFSR2(majority):
    if L[10] == majority:
        self.applyClock()
def clockLFSR3(majority):
    if L[10] == majority:
        self.applyClock()