Statistical Tests for Pseudorandom Functions

Question

Say I have an implementation of a potential Pseudo-Random function and I want to test whether my implementation does at least not contain any obvious flaws. As far as I understand, in other cryptographic settings, statistical tests are employed to ensure the correctness of the encryption algorithm. What kind of statistical tests could I use for Pseudo-Random functions?

Answer 1

Nobody uses generic statistical tests to verify correctness of encryption algorithms.

• To verify correctness of an implementation, engineers write proofs of correctness for their code, tr running it on known-answer tests, confirm round-trips on randomized inputs, etc.

  None of this involves statistical tests, since the point is to implement a specific mathematical function, not to sample stochastically from a distribution—indeed, if you did use generic statistical tests you'd have to decide what to do in the case of false alarms, which would be an absurd way to approach verification of software implementing deterministic mathematical functions.

• To assess security of a cryptosystem, cryptographers study specialized statistical tests.

  Assuming, following the advice of Kerckhoffs, that the adversary knows the system, what's the best they can do to attack it with that knowledge? Generic statistical tests like $\chi^2$ tests are stupid because they don't even know the system. For example, here's a test for distinguishing a 256-bit AES-CTR stream under a uniform random key from a uniform random 256-bit string:

  1. Guess a key $k$ uniformly at random.
  2. Check whether the string $s = s_1 \mathbin\| s_2$ is of the form $\operatorname{AES}_k(0) \mathbin\| \operatorname{AES}_k(1)$. If it is, guess AES-CTR; if it isn't, guess uniform random.

  
  This test has distinguishing advantage $2^{-256}$ (or $2^{-128}$ if you use AES-128 instead of AES-256, which I don't recommend[1]), so the best distinguishing advantage for AES can't be worse than $2^{-256}$, but a lot of smart cryptanalysts haven't found a way to do any better than that. Obviously, you could spend more computation—try it twice, with two different keys $k_1$ and $k_2$—to raise the advantage linearly, so this number should be qualified with a cost factor.

Any putative pseudorandom function family should come either with the paper droppings of a horde of cryptanalysts demonstrating failure to find a better-than-generic distinguisher, or with a proof of a theorem relating the security of the PRF to the security of some underlying primitive. For example, the best PRF-advantage attainable against AES by any distinguisher making $q$ queries is bounded by the best PRP-advantage attainable against AES, which cryptanalysts have studied for decades now, plus $q(q - 1)/2^{129}$ because AES is always a permutation.

So, put your generic statistical tests in the garbage. Find the literature on the putative PRF. Write a proof of correctness of your code.

Answer 2

You're right. A random stream should be identical to a well encrypted stream . To test it you can pass a plain counter through it, as $F(counter)$. The output should be pseudo random. Therefore the first port of call for all RNGs should be ent. There are few 'simple' design errors that can fool an ent test. You can test up to 2GB of data, and a typical pass result is:-

Entropy = 8.000000 bits per byte.

Optimum compression would reduce the size
of this 1073741824 byte file by 0 percent.

Chi square distribution for 1073741824 samples is 271.72, and randomly
would exceed this value 22.54 percent of the times.

Arithmetic mean value of data bytes is 127.5000 (127.5 = random).
Monte Carlo value for Pi is 3.141575564 (error 0.00 percent).
Serial correlation coefficient is -0.000034 (totally uncorrelated = 0.0).

Just be aware that you need at least 500kB of data for the result to be meaningful. This example is 1GB from /dev/urandom. An alternative at this point in your function's evolution is the FIPS 140-2 RNG test as part of the Rng-tools suite. It tests them in blocks of 20kb. Chances are that you'll know about $F$ at this stage.

After that, you can advance to more comprehensive tests like TestU01, Diehard(er), NIST SP 800-22, etc. Just be aware of the required sample sizes, as some of the tests can be really greedy with Dieharder a case in point. It's worth noting that you should expect some tests to fail. Do not despair, as that's as it should be as randomness is pesky.

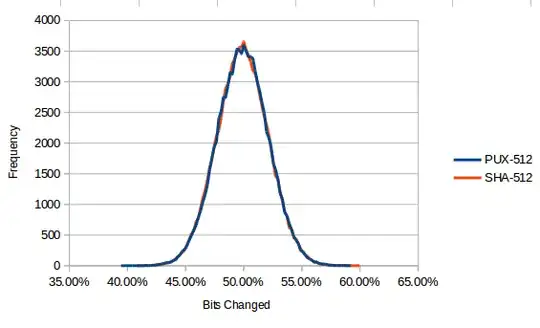
You might also want to look at the avalanche effect and it's calculation. It's simple (based around xored random numbers) and if $F$ is working, you'll get a normal graph centred on 50% like:-

with (in bits) $ \sigma = \frac{\sqrt{block width}}{2} $. As my esteemed friend points out, statistical testing doesn't address all major security aspects of $F$. However it addresses some, and it does form a very good check on the mechanics of your algorithm.