Security of (2,2) Shamir's visual secret sharing scheme : How are the 2 shares random?

Question

From the Visual Cryptography by Shamir and Noar.

Let us take the pixel expansion as 2. Therefore, each pixel will be represented by 2 pixels (also called as subpixels) in a share. Since this is a (2,2) scheme, we will have 2 shares. In order to create share1 for a white pixel, a fair coin is tossed with 2 possibilities of subpixels - Black&White or White&Black - either one of these 2 choices is chosen to represent a white pixel. It is clear that Share1 is random.

In order to create share2 for a white pixel, is a coin tossed again? If yes, then how is reconstruction of a white pixel assured? If no, then how is share2 random? Assuming that in the reconstructed image, the white pixel will be 50% black and 50% white.

Answer 1

First of all, coin tossing represents a uniform random generator. Therefore, the selections are assumed to be uniform.

In order to create a share for a pixel, as you mentioned, a pixel split into two subpixels. A share for

• a white pixel can be $[(B|W),(B|W)]$ or $[(W|B),(W|B)]$
• a black pixel can be $[(B|W),(W|B)]$ or $[(W|B),(B|W)]$, where in $[(x,y)]$, $x$ represents the color of left pixel and $y$ represents the color of right pixel.

or, one can see from the image;

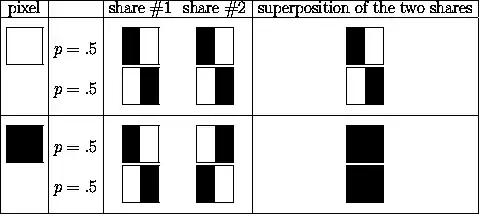
The superposition is putting the images on top of each other. White shares construct a half white and half black square and black shares construct a black square. When the selection is random, the shares are indistinguishable from being white or black.

How a share is constructed

For each pixel, toss a coin to select a row. For example, assuming that when the toss result is Tail, we select the first rows;

• for white pixels, select $[(B|W),(B|W)]$ and
• for black pixels, select $[(B|W),(W|B)]$.

Similarly, for Head result, we select the second rows.

• for white pixels, select $[(W|B),(W|B)]$ and
• for black pixels, select $[(W|B),(B|W)]$.

The confusion

If we toss a coin for the second share (instead of selecting the share together), then for example; for a white pixel after a Tail (select first row $(B|W)$), we may select the second row with a Head then the white pixel will be shared as $(B|W)$ and $(W|B)$. In superposition, however, this constructs a black pixel $(B,B)$. Therefore, they must be selected together.

Share 1 and share 2 are random in group-wise.