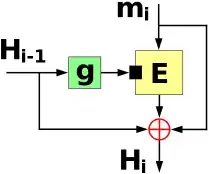
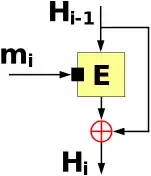
The only Miyaguchi–Preneel MD hash I know is Whirlpool. I suppose there are likely others.
Why do most MD hashes choose Davies–Meyer?
If anything, Davies–Meyer relies on related-key resistance while Miyaguchi–Preneel relies on chosen-plaintext resistance. The former ought to be far more difficult to achieve.
So I'm curious about the rationale.
Edit:
After some further research all I could find was the fact that Davies-Meyer is more efficient because it allows you to stretch the message block based on how the key schedule of the underlying block cipher works. Whereas Miyaguchi–Preneel forces you have
length(key) = length(message block) = length(output)
and deviating from that while possible (with padding) complicates security. So I guess the question is whether that the only reason? Performance? Flexibility? SHA2 may not be able to have variants (eg: 256, 512) as easily with Miyaguchi-Preneel.