Assume I have a list of plaintext text and its corresponding ciphertext which was created using a specific key with AES in ECB mode.
Can I recover that key?
If, how big does the list of plaintext and matching ciphertext have to be to be able to find it in a feasable amount of time (say in 1 or 2 hours)?
Assume I have a list of plaintext text and its corresponding ciphertext which was created using a specific key with AES in ECB mode.
Can I recover that key?
No. This is what is referred to as a known plaintext attack, and secure block ciphers are designed to prevent exactly this kind of attack. This answer on the Mathematics Stack Exchange goes into more detail about the notion of IND-CPA ("indistinguishability") which AES is conjectured to meet and how that implies that a known plaintext attack is impossible.
What is the simplest attack is the Brute Force Attack. However, it is infeasible to brute-force even AES-128 bit, AES also supports 192, and 256-bit keys sizes. To break the AES-128 with brute force, you need to execute $2^{128}$ AES operations, today's top computers can reach $2^{63}$ around one hour. However, reaching $2^{128}$ is beyond classical computing.
In brute-force with only one key, the number of elements in your list is not really important, a few will be enough to uniquely determine the key.
In your case, the problem is the key-size. You have to check every possible key to match one of your plaintext-ciphertext pair;
for each k in possible keys
if E(k,P1) == C1
testWithSomeOtherPair(k)
Once you found you can verify with the other plaintext-ciphertext pairs.
Note: there are other types of attacks (related-key attacks which are not related to your case.) faster than the brute-force for AES-192 and AES-256 with $2^{176}$ and $2^{99.5}$-time, respectively. But they are still infeasible to reach. For AES-128, the fastest known is the Biclique attack with $2^{126.2}$ and that is still infeasible and in practice, the brute-force may still beat the Biclique attack which requires $2^{88}$-data and $2^8$-memory. Biclique attack for AES-192 and AES-256 runs with $2^{189.7}$ and $2^{254.4}$ computational complexity, respectively.
As the other answers have mentioned, you basically have no hope of executing a key-recovery attack. This does not mean, however, that you should give up and go home. Key recovery is not the only kind of attack, and the information you have available gives you a different attack, which allows you to decrypt some ciphertexts without using the key. The other answers don't mention the fact that this encryption scheme uses ECB-mode.
As you mentioned in a comment, you have a list of valid and related plaintext/ciphertext pairs, and you have another ciphertext, and you want to make an educated guess as to its corresponding plaintext.
The use of ECB mode gives us a credible attack. Recall the operation of ECB:
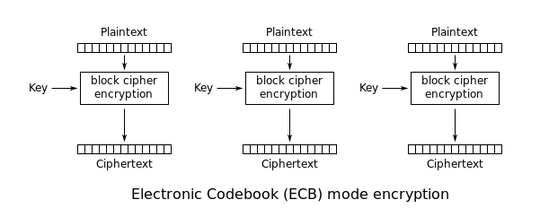
Each plaintext block is fed into the block cipher, and the corresponding ciphertext block is just its output. This means that, wherever the plaintext block appears in whichever message, the output ciphertext will always be identical.
AES usually uses a 128-bit block-size, which is 16 bytes. You might have 192- or 256-bit AES, but I don't see these quite so often. This means that if you split your plaintexts and ciphertexts into 16-byte chunks you might see see that in one chunk the plaintext 11 22 33 44 55 66 77 88 99 00 aa bb cc dd ee ff corresponds to the ciphertext 12 34 56 78 90 ab cd ef fe dc ba 09 87 65 43 21. Now, whenever you see that ciphertext in any message ever, you can map it back to that plaintext!
Now, you mentioned that this was a homework question. You should write some software to do this for you, and exactly what that looks like I'm not going to say because we aren't a homework solving service, but hopefully you should be able to use this insight to recover your flag.
Your next lessons are probably going to talk about CTR and CFB encryption modes, which stop this attack from working.
