The Alternating Step Generator was proposed by Christoph G. Günther: Alternating step generators controlled by de Bruijn sequences, in proceedings of Eurocrypt 1987. It's perhaps the conceptually simplest CSPRNG producing bits at a constant rate. Its best-known cryptanalysis is by Shahram Khazaei, Simon Fischer, and Willi Meier: Reduced Complexity Attacks on the Alternating Step Generator, in proceedings of SAC 2007.
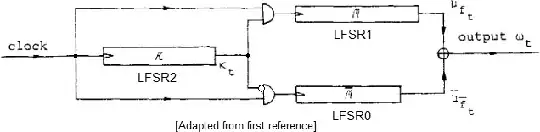
The ASG combines three Linear Feedback Shift Registers. To produce a bit:
- advance LFSR2
- according to its low-order bit, advance LFSR0 or LFSR1
- output the XOR of the low order bits of LFSR0 and LFSR1
The key is the initial state of the LFSRs (assumed to be random and independent bits, save for the state of each LFSR not being all-zero). It is customary to use primitive binary polynomials of distinct degree $n_i$. In the initial exposition, LFSR2 is modified to generate a de Bruijn sequence, that is the output sequence has an extra zero inserted after $n_2-1$ consecutive zeroes. But this detail makes no cryptanalytic difference, since that point in the sequence is reached with negligible probability for $n_2$ large enough for security.
Would using binary trinomials sizably reduce the cryptanalytic resistance of the ASG?
The rationale to want to use trinomial:
- it minimizes implementation cost in hardware (each additional coefficient cost an XOR gate), and the number of reads in a software implementation using indexes in circular buffers;
- it reduces the choice, allowing to make the primitive trinomials "nothing up my sleeve";
- we can use the compact table of primitive binary trinomials compiled by Jörg Arndt.