Perform ENT / Dieharder on raw entropy or on whitenened entropy?

Question

In this question about hardware random number generator, a discussion about the following question has been started: In order to test RNG's and entropy's quality, should test suites like ENT and Dieharder be applied on raw entropy or on whitened entropy?

Answer 1

It depends on the goal of performing the test:

• If the goal is to test for a problem in the whitening, then the test should be run on the whitened output, of course. If the test fails (more often than predicted by the P-value), the whitening is demonstrated bad. If the test pass, we can deduce nothing cryptographically useful (the source or the whitening could be badly defective, or/and the tested output could be totally predictable by who knows how it was generated). The test is slightly less pointless if the source is replaced with a very low entropy source during the test.
• If the goal is to test for a problem in the noise source, then the test should be run on the noise source before whitening. If the test fails (more often than predicted by the P-value), then the noise source is demonstrated not good enough to be used for cryptographic purposes without whitening (but it might still be excellent and perfectly usable with whitening; many if not most good truly raw sources fail Dieharder, some fail ENT). If the test pass, we can deduce nothing cryptographically useful without knowledge of how the noise source is actually operating, and of how the test works.
• If the goal is to pass a conformance test, then the rule it to perform things as satisfies the person with the rubber stamp. If s/he does not care, the easy route is to use the whitened output, so that a good whitening is a sufficient way to pass the test, irrespective of the source. I guess that happened (for FIPS 140-1 and -2 conformance, some tests where mandatory and too stringent for most practical sources; reason prevailed and the tests have been removed, yet the tests remain what some suppliers of RNGs brag about).

There is no other rational goal met by solely performing a RNG test on a sequence, when it passes. Repeating the first bullet: if the test is a blackbox test on the whitened output of a source, then a pass indicates nothing cryptographically useful about the source, the whitening, or the combination.

---

I have assumed the test is at least correct (and in particular, fails with likelihood comparable to its stated P-value when given truly random input), and correctly used. That's more often than not disproved by repeatedly applying the test to the output of a known-good CSPRNG. The test should pass (with occasional failures per its P-value) regardless of the CSPRNG's input (as long as it is arbitrary rather than tailored to the test being tested).

---

Note: ENT is a terrible test from a cryptographic standpoint, especially for a whitened source. For example, a PRNG that 90% of the time outputs a byte equal to one more (modulo 256) than the previous one, and is random the other 10%, is still considered perfectly OK.

Note: Temperature or process variations, EMI, aging, adversarial influence, or Murphy's law, can ruin a noise source. In cryptographic devices it is thus critical that the proper operation of the noise source is continuously monitored. A technically valid security certification process aims at checking source, whitening, and that monitoring puts the whole device in a safe state (as a minimum: squelches the whitened output) on detection of failure. This goal is antagonist to field reliability, and it is hard to get both.

Answer 2

Ideally a whitening algorithm passes data through cryptographic algorithms, rather than doing something simple (like Von-Neumann's unfair coin de-biasing algorithm or reading the least significant bit of noisy analog-to-digit converters.) If this is the case (and it should be), then testing post-whitened data is useless.

If I were responsible for designing a hardware RNG, I would use a hybrid system which processed input from entropy sources with a hash function or sponge. (All of the data, not just one bit cherry picked because it looks like it's the most random input bit.)

This process can turn an arbitrarily long input into a fixed size output. I would use that output to initialize a CS-PRNG (which will have output indistinguishable from true random) and use that PRNG to provide random numbers to the end user at a rate faster than a pure hardware RNG could provide and with a higher degree of confidence in the whitening process than alternative algorithms.

The hash based entropy collector can be reset immediately after seeding the CS-PRNG and can be used to reseed the PRNG as soon as it re-collects enough entropy again to have totally unpredictable output again.

That solution makes testing post-whitening output pointless. A hash function that behaves like a random oracle (a stronger form of the idea of "the avalanche property" of non-cryptographic hashes) won't exhibit statistical behavior that is so bad that black box statistical tests can detect it. Same for the PRNG.

The question you have to answer with this method is "Have I hashed enough input since I last seeded my PRNG to re-seed it now?" And that answer depends on how much entropy is contained in the hash input string.

The way to answer that question is NOT with software like Diehard or it's successors. Tests need to be tailored to the type of noise source you are using. In addition to tailored statistical tests, you should build a model that lets you test if the hardware is working as expected. It is risky to look at a signal, conclude it looks random, then try to output whitened data at approximately the same rate that raw signals are read in. If your guess is wrong or there is a slight drift in noise signals over time you'll have problems.

It is okay if an input signal has a low ratio of (min-)entropy to input bit length. Hash based randomness extractors can process long input strings very quickly. You can read in much more signal than you really need, the primary side effect is that the hash output will be even less predictable than you thought. (With a tiny increase in latency between the time you turn it on the HWRNG and when it can first emit output.)

Over-estimating entropy is bad because it makes output more predictable. Under-estimating just leads to overkill "a higher safety margin".

Using statistical tests designed for non-cryptographic PRNG is a bad method of estimating entropy. They pass PRNGs with a constant seed after all. (Which is a system with zero entropy.) You should NOT rely on ENT or Diehard. DON'T use them with cryptography for anything, except possibly as a sanity check.

---

Note: Diehard is ancient. (Meaning it's 90's technology.) It was re-implemented in the "Dieharder" package which includes many additional tests. Dieharder is better but not great.

TestU01 is probably the most reliable successor to Diehard. There is also "PractRand" which is newer but I'm uncomfortable with calling reliable based on the source code I looked into of some older version.

ENT is way less useful than you would assume based on the name. It consists of only a frequency test and a file compression ratio based test. It is so simple (read that as "limited") that it should be avoided.

---

The problem with using tests designed for PRNGs is that they are not designed for arbitrary signals. With the exception of PractRand claiming to support 64 bit generators, the other PRNG tests are based on inputs modeled either as a sequence floating point values in the range [0,1] or a sequence of words up to 32 bits long.

You have to be able to digitize signals from entropy sources. Unless your entropy source naturally lends itself to be converted to zeros and ones (like a ring oscillator) or to a floating point (noise read in via unusually high-resolution analog-to-digital converters) it's difficult to determine how you're even going to convert input signals to a format that would make sense to use with black box (non-crypto) PRNG tests.

MOST IMPORTANTLY, a negative result from these test applications (meaning no biases found) DOES NOT tell you that the (pre-whitened) input has sufficient entropy. (Entropy meaning unpredictability.) A positive test on raw input data can be interpreted as "the unwhitened data definitely would not make a good RNG". But a negative test cannot be interpreted to mean anything.

Answer 3

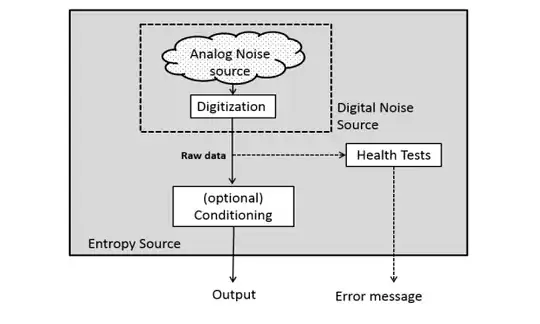
It may be useful to illustrate how a TRNG works:-

And perhaps more importantly, you have to realise that random means random, or uncertain. It absolutely does not mean independently and identically distributed random numbers (non IID). A gangster's lucky die with a corner filed off is random. It is biased yes, but it is nevertheless random as no particular outcome can be predicted with 100% certainty. So it might be used as the analogue entropy source in the above diagram. Similarly you might use a Zener diode or a photon detector for this purpose.

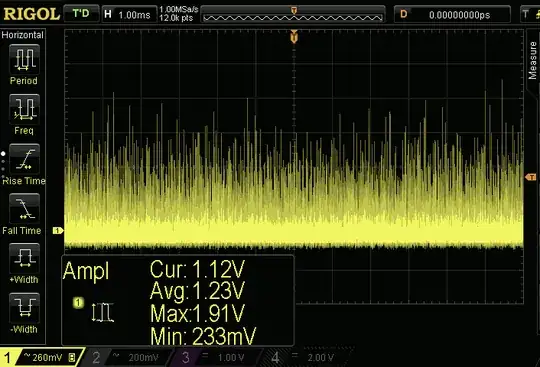
The (digitised) raw data output from the noise source, is called the entropy. If the source is a Zener, the raw might look like the following if viewed on an oscilloscope:-

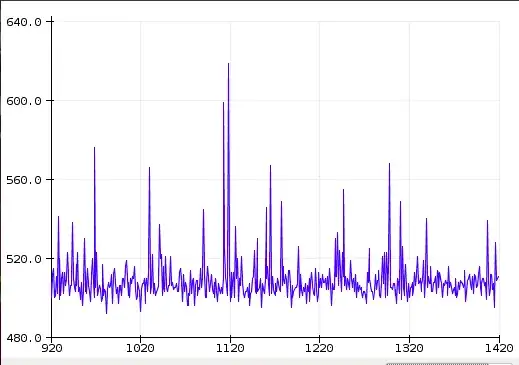
Notice the asymetry in relation to the little yellow arrow with the "1" in it. That's the zero reference. And this is how it looks following digitisation:-

You can clearly see that it's highly biased and correlated, and the values are 10 bit samples. This is the entropy source within a real TRNG on my wall and is very non IID. It's a standard avalanche effect log normal distribution plus correlation of readings in actuality. Most entropy sources are non IID, although some get pretty close to IID. The Quantis laser devices get to > 0.94 bits/bit. It is random at this raw data stage, but not IID as required for the final output of a TRNG. My example trace is conservatively about 1.5 bits /sample entropy, or ~15% purity.

And so to ent /Diehard. What possible information could be gained by running an ent test on this raw data? It will fail massively, as it should. Diehard and all other randomness tests will also fail. Such tests cannot even accept 10 bit worded data. And the data might be received in ASCII comma separated format or as a Numpy array, further invalidating testing. The reason is in the name "Randomness Test". This raw entropy is not even close to IID random, which is the purpose these tests are designed for.

And almost finally, the following is an ent test of the above raw entropy:-

Entropy = 5.840091 bits per byte.

Optimum compression would reduce the size
of this 500000 byte file by 26 percent.

Chi square distribution for 500000 samples is 6926978.44, and randomly
would exceed this value less than 0.01 percent of the times.

Arithmetic mean value of data bytes is 160.3918 (127.5 = random).
Monte Carlo value for Pi is 1.805719223 (error 42.52 percent).
Serial correlation coefficient is 0.286267 (totally uncorrelated = 
0.0).

The test has failed. So will all other randomness tests. Even the entropy measurement of 5.84 bits /byte is incorrect as ent is not an entropy measurement tool. A live source of raw entropy can be found here. What use running diehard on the linked data that only ranges 50 units at most? It will fail with a string of p = 0s or p = 1s. As expected.

In summary, you check the final output of a TRNG with these tests to ensure that the whole system (including conditioning) works properly. And to a lesser extent, the tests might also pick up a failed entropy source but that is really the purview of Health Tests in the initial diagram.