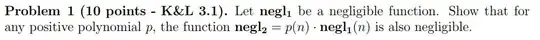3

My question is about proving that a function is negligible if it is ran polynomial number of times.

question

This my solution: By the definition of negligibility, we have $negl_1(n) < 1/p'(n)$ where $p'(n)$ is any polynomial. We multiply $p(n)$ both sides: $p(n)*negl_1(n) < p(n)/p'(n)$.

We let $p'(n)>>p(n)$. There is always a $p'(n)$ that satisfies this inequality. Thus, $negl_2(n) = p(n)*negl_1(n)$ is negligible.

Is my solution correct?

Mike Edward Moras
  • 18,161
  • 12
  • 87
  • 240
Mitch
  • 31
  • 2

2 Answers2

3

Your solution is not correct. You have to show that $\mathbf{\text{negl}_2}$ satisfies the definition of negligible functions and what you "showed" actually is that given any sufficiently large polynomial $p'(n)$, it holds that $\mathbf{\text{negl}_2} < \frac{p(n)}{p'(n)}$.

I see two easy ways of solving that exercise:

  • Try to prove it by contradiction supposing that $\mathbf{\text{negl}_2}$ is not negligible and then finding a polynomial whose inverse is asymptotically smaller than $\mathbf{\text{negl}_1}$.
  • Try to prove it directly: from any given polynomial $p'(n)$, you know that $p(n)p'(n)$ is a polynomial, therefore, $\mathbf{\text{negl}_1}$ must be smaller than $1 / (p(n)p'(n))$ for all $n$ bigger than some $n_0$...
Hilder Vitor Lima Pereira
  • 7,476
  • 1
  • 25
  • 45
0

I'll try to solve this and I'll be happy if someone would be able to say it's correct or not.

Let p be a positive polynomial. Since $negl_1$ is negligible there's a number N such that for any n>N we have: $$negl_1(n) < \frac{1}{p(n) * p(n)}$$

(as polynomial * polynomial is polynomial)

This gives us that for any n>N we have:

$$negl_2(n) = p(n) * negl_1(n) < p(n) * \frac{1}{p(n) * p(n)} = \frac{1}{p(n)}$$

And we got that $negl_2$ is a negligible function as well.

GMathWagon
  • 11
  • 1