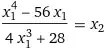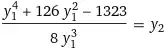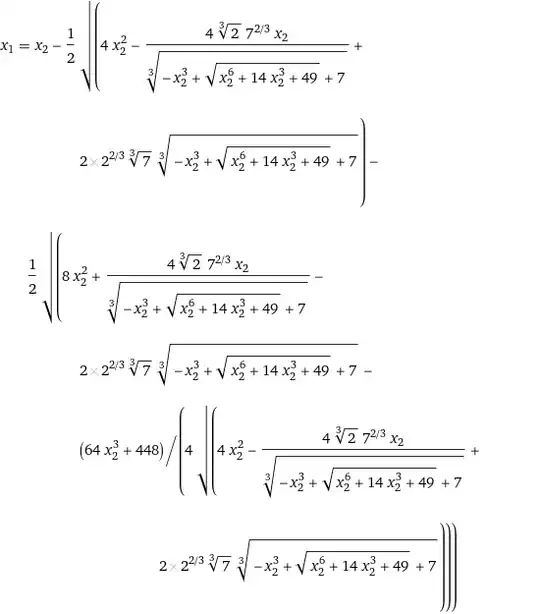Elliptic Curve - Divide by 2

Question

Can anyone tell me the specific equations and steps for dividing a point on an elliptic curve by 2?

For instance, I have the point $(P_x, P_y)$, and I would like to find the point $(R_x, R_y)$ which when doubled yields $(P_x, P_y)$.

It was suggested that I use the point doubling equations and solve, but I am looking for the specific equations and steps and perhaps a reference to thorough discussion of the topic.

Thanks for your time.

EDIT: I was under the impression that it would be the same steps for all curves. In this instance I am trying to do it on the secp256k1 curve.

score 11 · Accepted Answer · answered Jan 29 '18 at 14:35

There are two strategies to do what you want.

The first one being to find the group order $q$ and then compute $i=2^{-1}\bmod q$. When you then multiply your point $P$ by $i$ you get $Q=[i]P$ with $[2]Q=[2i]P=[(2\cdot 2^{-1})\bmod q]P=P$ as desired. This general strategy works for any finite group (as long as $q$ is not even) and was quickly pointed out by fgrieu in the comments.

The second way goes as follows:

Find out the equation for your curve. For secp256k1 this is $y^2=x^3+ax+b$ a.k.a. "Short Weierstrass Form".
Go to the explicit formula database and select the relevant curve.
Take the affine doubling equation and plug it into your favourite tool for solving algebraic equations and tell it to solve for the coordinates on the left side.
You should now receive a result. Because all fields are equal when it comes to the transformations carried out, you can just take the resulting formula and "easily" translate it to work over your finite field.

Michael Zieve · Answer 2 · 2022-12-23T15:09:47.517

Here are explicit equations in characteristic not $2$, from the paper "Division by 2 of rational points on elliptic curves" by Bekker and Zarhin (St. Petersburg Math. J. 29 (2018), 683-713).

If the elliptic curve $E$ has equation $y^2=p(x)$ where $p(x)$ is a degree-$3$ polynomial, then let $r_1,r_2,r_3$ be the roots of $p(x)$. For any point $P=(P_x,P_y)$ on $E$ with $P_x\notin\{r_1,r_2\}$, let $s_1$ and $s_2$ be any square roots of $P_x-r_1$ and $P_x-r_2$, respectively, and put $s_3:=-P_y/(s_1s_2)$. Write $u:=s_1+s_2+s_3$ and $v:=s_1s_2+s_2s_3+s_3s_1$. Then $R:=(P_x+v,-P_y-uv)$ is a point on $E$ such that $2R=P$.

Note that there are known formulas for the roots of a degree-$3$ polynomial, in terms of square roots and cube roots of certain elements. Also, the hypothesis $P_x\notin\{r_1,r_2\}$ can always be achieved by relabeling the $r_i$'s if needed. So this recipe really does yield explicit equations.