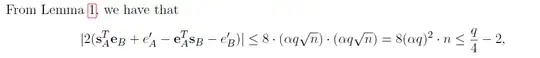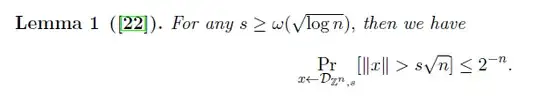In this paper (A simple provably secure key exchange by Ding et al.) At page number 8, the author gives correctness of the technique as follows
then SK A = SKB with overwhelming probability i.e. if Alice and Bob run the protocol honestly, then they will share an identical key.
The above equation uses Lemma 1 which is as follows
How does the author deduce the above equation using Lemma 1. This equation gives correctness of the technique. Can anyone please help.
First: Lemma 1 says that $||\mathbf{x}|| \leq \alpha q \sqrt{n}$ with overwhelming probability if $\mathbf{x}$ is drawn from the discrete Gaussian since $\frac{1}{2^n}$ is negligible.
Next, from properties of absolute values, $|a + b| \leq |a| + |b|$. So, leaving the $2$ out for now and writing $\mathbf{s_A}^T\mathbf{e_B}$ as $\mathbf{s_A}\cdot\mathbf{e_B}$:
$|\mathbf{s_A}\cdot\mathbf{e_B} + e'_A + \mathbf{s_B}\cdot\mathbf{e_A} + e'_B| \leq |\mathbf{s_A}\cdot\mathbf{e_B}| + |e'_A| + |\mathbf{s_B}\cdot\mathbf{e_A}| + |e'_B|$.
Now, for Euclidean norms, Cauchy-Schwarz says $|\mathbf{a\cdot b}| \leq |\mathbf{a}|\cdot |\mathbf{b}|$, so we have, for example, $|\mathbf{s_A}\cdot\mathbf{e_B}| \leq |\mathbf{s_A}| \cdot |\mathbf{e_B}| \leq (\alpha q \sqrt{n})\cdot (\alpha q \sqrt{n})$, the last inequality coming from Lemma 1.
Let's tackle $e'_A$ and $e'_B$. I could sample a vector $\mathbf{e'}$ from $\mathcal{D_{\mathbb{Z^n},\alpha q}}$ and Lemma 1 would apply to it; if $e'_A$ is a member of $\mathbf{e'}$, it is certainly smaller than $||\mathbf{e'}||$:
$|e'_A| \leq ||\mathbf{e'_A}|| \leq \alpha q \sqrt{n} \leq (\alpha q \sqrt{n})\cdot (\alpha q \sqrt{n})$. Same for $e'_B$.
Thus I have four terms, all $\leq (\alpha q \sqrt{n})\cdot (\alpha q \sqrt{n})$. Multiply back in that $2$ and you have the result.
They do a similar procedure later on in Section 4, and explicitly write out norms, for future reference.
This lemma is used to conclude that a sample from $\mathcal{D}_{\mathbb{Z}^n,\alpha q}$ is (with overwhelming probability) less than or equal to $\alpha q \sqrt{n}$.
Now, because all values $\textbf{s}_{\textbf{A}},\textbf{s}_{\textbf{B}},\textbf{e}'_{\textbf{A}},\textbf{e}'_{\textbf{B}}$ are sampled from $\mathcal{D}_{\mathbb{Z}^n,\alpha q}$ , so $\textbf{s}_{\textbf{A}}^T\textbf{e}_{\textbf{B}}$ is less than or equal to $(\alpha q \sqrt{n})(\alpha q \sqrt{n})$. This bound is also true for each of other values $\textbf{e}_{\textbf{A}}^T\textbf{s}_{\textbf{B}}, \textbf{e}'_{\textbf{A}},\textbf{e}'_{\textbf{B}}$ and so the upper bound is determined.
