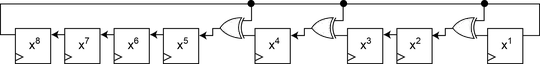Galois LFSR Subsequence Periodicity

Question

I had the following questions -

1. Concerning generating sequences of bits $\textbf{x} = ( x_{0},x_{1}, ... , x_{n-1})$ where the $x_{i} \in \{0,1\}$ are considered coefficients of a polynomial in $\gamma$ (i.e. a polynomial of form $x_{0} + x_{1}\gamma^{1} + ... + x_{n-a}\gamma^{n-1}$) where $\gamma$ is the root of a polynomial $ \Lambda(\gamma) = c_{0} + c_{1}\gamma + ... + c_{n}\gamma^{n} = 0$, $c_{i} \in \{0,1\}$ (i.e. $\textbf{x}$ is an element in a Galois extension), I understand that all the elements of this extension (i.e all possible n bit binary strings) can be generated through the relation $\textbf{x}_{j} = \gamma \textbf{x}_{j-1} \textbf{mod} \space \Lambda(\gamma)$ for correct choice of $\Lambda(\gamma)$, the "period" of this generator is $2^{n} - 1$ after which the recurrence relation "wraps around" the ring and generates the first element over. This is described on page 11 here. If we consider $k$ bit subsequences of this $n$ bit string, is it possible to derive the period for a such a subsequence?

2. Is there a reference that concretely describes how to go from a construction above based on arithmetic in the field extension to the familiar Galois LFSR as described here?

Answer 1

Although I cannot speak to the first part of your question, I can answer the second part. Also, I have never seen a formal explanation of how to map polynomials to a LFSR. In retrospect, I honestly do not know if the polynomials that I have been given were picked because it was known that they would map to circuits, but here is how I do it.

As our example, we will start with the irreducible polynomial used in AES:

$$P(x)=x^8+x^4+x^3+x+1$$

I drop the $+1$, which is the $x^0$ term. This gives me 8 total flip flops: $x^8,x^7,x^6,x^5,x^4,x^3,x^2,x^1$. Due to the form of $P(x)$, I expect XOR feedback taps after $x^8,x^4,x^3,x^1$, which tap $x^8$ becomes just a feedback line as it goes to nothing. The resulting circuit is:

In the circuit above, the data moves to the left from the right. Taking the initial condition for AES as 0x01, we get the logic of:

01: 0x01
02: 0x02
03: 0x04
04: 0x08
05: 0x10
06: 0x20
07: 0x40
08: 0x80
09: 0x1b
10: 0x36
11: 0x6c
12: 0xd8
13: 0xab
14: 0x4d

This method has worked every time that I have implemented a LFSR as an irreducible polynomial. The first time I looked at the problem was with a simple polynomial and the answer was just "obvious". I carried that system forward to ever other time and so far, so good.

Additions, comments and a proper method would be welcome.