What's the difference between RSA and Diffie-Hellman?

Question

I've been reading the same thing on a lot of websites: RSA is for communication using the public and private key for both the server and client, whereas Diffie-Hellman is just for exchanging the same secret key that will then be used for both encryption and decryption. But they both depend on the same math.

E.g: This question on Quora:

Then I was confused when I read that RSA shares a master and pre-master key, as well. As described in this answer.

The question here is: Does RSA use the public and private key to encrypt the whole conversation, or is it used just to encrypt a key, then the encryption depends on that symmetric key? And if it was used to encrypt the key using the same math as in Diffie-Hellman, what is the difference anyways?

Answer 1

Diffie-Hellman Key Exchange

Problem: We have a symmetric encryption scheme and want to communicate. We don't want anybody else to have the key, so we can't say it out loud (or over a wire).

Solution/Mechanics:

1. We each pick a number, usually large, and keep it a secret, even from each other. I'll pick $x$, and you'll pick $y$.

2. We agree on two more numbers, both prime, which anybody can know. We'll call them $g$ and $n$.

3. I'll calculate $g^x\bmod n$ and tell you my answer. You'll calculate $g^y\bmod n$ and tell me your answer.

4. Our shared key is $g^{xy}\bmod n = (g^y\bmod n)^x\bmod n = (g^x\bmod n)^y\bmod n$.

RSA Asymmetric Encryption

Problem: I want anybody to be able to encrypt a message, but I'm the only one who can decrypt it. I don't want to share decryption keys with anybody.

Solution/Mechanics:

1. I choose two large primes, $p$ and $q$.

2. I calculate $n$ such that $pq = n$.

3. I calculate $t$ such that $(p-1)(q-1) = t$.

4. I choose an integer $e$ that is both less than $t$ and coprime with $t$.

5. I find $d$ such that $d$ is the multiplicative inverse of $e$ modulo $t$.

6. I release $(e, n)$ as my public key, and retain $(d, n)$ as my private key.

7. When you communicate with me, you treat your message as a large number $m$. The ciphertext $c$ is given by $c = m^e\bmod n$, and decrypted by $m = c^d\bmod n$.

Answer 2

In practice, in situations like TLS, public key encryption will be used to encrypt a secret for encrypting the actual messages, as part of a hybrid cryptosystem. This is done because Asymmetric cryptography is significantly slower than symmetric cryptography.

However, there are other cryptosystems and applications that utilize public key encryption directly. As an example, ransomware is not concerned with how long it takes to encrypt something, and it benefits immensely from not possessing the decryption key.

There are also cryptographic logging schemes that make use of public key encryption directly:

Due to the forensic value of audit logs, it is vital to provide compromise resiliency and append-only properties in a logging system to prevent active attackers. Unfortunately, existing symmetric secure logging schemes are not publicly verifiable and cannot address applications that require public auditing...

So whether or not public key encryption is used for key exchange or on the data itself is actually a matter of where the tools are being used.

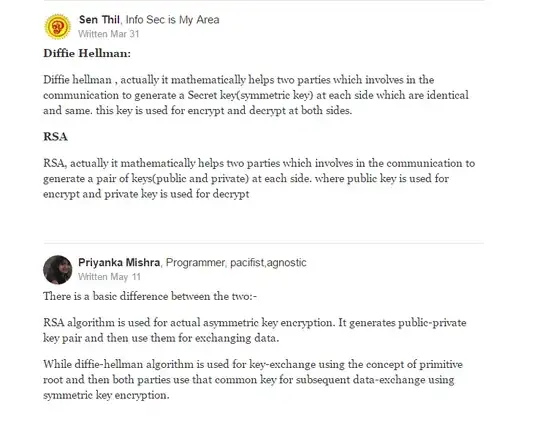
RSA and Diffie-Hellman are based on different but similar mathematical problems. While they both make use of modular exponentiation, exactly what they do/why they work is different. This is evident when you look at how to attack each one: RSA is threatened by integer factorization, while DH is threatened by discrete logarithms.

Additionally: DH is a "key exchange" algorithm, which is different then "public key encryption"; It allows you and another person to mutually arrive at the same piece of information, while nobody else can. It is more or less equivalent to using public key encryption on a random message. This is in contrast to public key encryption, where you get to select the message that both parties will be aware of.

Note that Diffie-Hellman can be turned into public key encryption.

tl;dr

Both use modular exponentiation to provide the main functionality (encryption/signature generation for RSA, key agreement for DH), but the underlying problem, the key pair generation and the security properties of the input/output are different