RSA-OAEP: How does it work?

Question

I was looking at this image about OAEP:

..and was wondering what was happening here.

1. We have a data block DB which consists of:

   • lHash: What is this and where does this come from?
   • PS: A string of zeros, but how much zeros?
   • M: clearly our message.

2. We have a seed which , is some random number. We put this seed into a MGF, a Mask Generating Function, and XOR the outcome with the MB. This is our maskedDB. Correct?

3. We put the maskedDB to the MGF again and XOR it with the seed. This is our maskedSeed.

4. For the final EM (encrypted message) we prepend some zeros. What do we do with EM then?

Answer 1

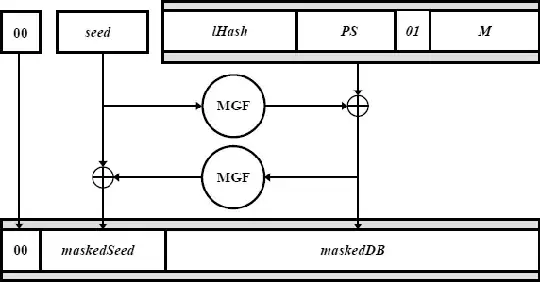
1a lHash: What is this and where does this come from?

That's in PKCS#1 v2.1: RSAES-OAEP-ENCRYPT ((n, e), M, L):

2a. If the label L is not provided, let L be the empty string. Let lHash = Hash(L), an octet string of length hLen (see the note below).

1b) PS: A string of zeros, but how much zeros?

Similarly for this question, lets look at the actual standard:

2b. Generate an octet string PS consisting of k - mLen - 2hLen - 2 zero octets. The length of PS may be zero.

2) We have a seed which , is some random number. We put this seed into a MGF, a Mask Generating Function, and XOR the outcome with the MB. This is our maskedDB. Correct?

Well, yes, but you XOR with DB, not with MB (whatever that is). It's in steps 2c..2f of the linked section of PKCS#1.

3) We put the maskedDB to the MGF again and XOR it with the seed. This is our maskedSeed.

4) For the final EM (encrypted message) we prepend some zeros. What do we do with EM then?

You continue with steps 3a..c and of course step 4 of the standard, which basically means:

• 3a) creating an integer from the octet string you've just constructed
• 3b) modular exponentiation with the public exponent and modulus of the public key (also known as raw or textbook RSA)
• 3c) creating an octet string from the result again

And 4, output the result (well...duh).